题目内容
10.已知在△ABC中,(2$\overrightarrow{BA}$-3$\overrightarrow{BC}$)•$\overrightarrow{CB}$=0,则角A的最大值为$\frac{π}{6}$.分析 用$\overrightarrow{AB}$,$\overrightarrow{AC}$表示出个向量,得出三角形三边的关系,利用余弦定理和基本不等式得出cosA的范围.
解答 解:∵(2$\overrightarrow{BA}$-3$\overrightarrow{BC}$)•$\overrightarrow{CB}$=0,即(2$\overrightarrow{BA}$-3($\overrightarrow{AC}$-$\overrightarrow{AB}$))•($\overrightarrow{AB}-\overrightarrow{AC}$)=0,
即($\overrightarrow{AB}-3\overrightarrow{AC}$)•($\overrightarrow{AB}-\overrightarrow{AC}$)=0,
∴${\overrightarrow{AB}}^{2}$-4$\overrightarrow{AB}•\overrightarrow{AC}$+3${\overrightarrow{AC}}^{2}$=0,
设A,B,C所对的边为a,b,c,
则c2-4bccosA+3b2=0,
又cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$,
∴b2-c2+2a2=0,即a2=$\frac{1}{2}$(c2-b2),
∴cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{{b}^{2}+{c}^{2}-\frac{1}{2}({c}^{2}-{b}^{2})}{2bc}$=$\frac{3{b}^{2}+{c}^{2}}{4bc}$≥$\frac{2\sqrt{3}bc}{4bc}$=$\frac{\sqrt{3}}{2}$.
∴0<A≤$\frac{π}{6}$.
故答案为$\frac{π}{6}$.
点评 本题考查了平面向量的数量积运算,解三角形等知识,属于中档题.

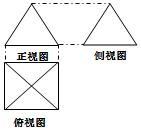 如果一个几何体的三视图如图所示,正视图与侧视图是边长为2的正三角形、俯视图轮廓为正方形,(单位长度:cm),则此几何体的侧面积是( )
如果一个几何体的三视图如图所示,正视图与侧视图是边长为2的正三角形、俯视图轮廓为正方形,(单位长度:cm),则此几何体的侧面积是( )| A. | .$2\sqrt{3}$cm | B. | .$4\sqrt{3}$cm2 | C. | 8 cm2 | D. | 12 cm2 |
| A. | $\frac{\sqrt{3}π}{9}$ | B. | 1-$\frac{\sqrt{3}π}{9}$ | C. | $\frac{\sqrt{3}π}{18}$ | D. | 1-$\frac{\sqrt{3}π}{18}$ |
| A. | 2 | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | 2或$\frac{2\sqrt{3}}{3}$ |
| A. | 此人第二天走了九十六里路 | |
| B. | 此人第一天走的路程比后五天走的路程多六里 | |
| C. | 此人第三天走的路程占全程的$\frac{1}{8}$ | |
| D. | 此人后三天共走了42里路 |
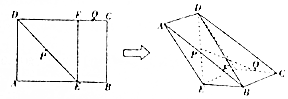 已知矩形ABCD中,E、F分别是AB、CD上的点,BE=CF=1,BC=2,AB=CD=3,P、Q分别为DE、CF的中点,现沿着EF翻折,使得二面角A-EF-B大小为$\frac{2π}{3}$.
已知矩形ABCD中,E、F分别是AB、CD上的点,BE=CF=1,BC=2,AB=CD=3,P、Q分别为DE、CF的中点,现沿着EF翻折,使得二面角A-EF-B大小为$\frac{2π}{3}$.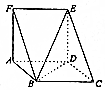 如图,三棱柱ABF-DCE中,∠ABC=120°,BC=2CD,AD=AF,AF⊥平面ABCD.
如图,三棱柱ABF-DCE中,∠ABC=120°,BC=2CD,AD=AF,AF⊥平面ABCD.