题目内容
14.在区间[0,1]上随机地取两个数x、y,则事件“y≤x5”发生的概率为$\frac{1}{6}$.分析 确定区域的面积,即可求出事件“y≤x5”发生的概率.
解答 解:在区间[0,1]上随机地取两个数x、y,构成区域的面积为1;
事件“y≤x5”发生,区域的面积为${∫}_{0}^{1}{x}^{5}dx$=$\frac{1}{6}{x}^{6}{|}_{0}^{1}$=$\frac{1}{6}$,
∴事件“y≤x5”发生的概率为$\frac{1}{6}$.
故答案为$\frac{1}{6}$.
点评 本题考查概率的计算,考查学生的计算能力,确定区域的面积是关键.

练习册系列答案
相关题目
5.中心在坐标原点的双曲线C的两条渐近线与圆(x-2)2+y2=3相切,则双曲线的离心率为( )
| A. | 2 | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | 2或$\frac{2\sqrt{3}}{3}$ |
9.将函数f(x)=2$\sqrt{3}$cos2x-2sinxcosx-$\sqrt{3}$的图象向左平移t(t>0)个单位,所得图象对应的函数为奇函数,则t的最小值为( )
| A. | $\frac{2π}{3}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{6}$ |
6. 某三棱锥的三视图如图所示,则该三棱锥的各个侧面中最大的侧面的面积为( )
某三棱锥的三视图如图所示,则该三棱锥的各个侧面中最大的侧面的面积为( )
 某三棱锥的三视图如图所示,则该三棱锥的各个侧面中最大的侧面的面积为( )
某三棱锥的三视图如图所示,则该三棱锥的各个侧面中最大的侧面的面积为( )| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{5}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\sqrt{2}$ |
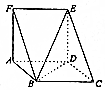 如图,三棱柱ABF-DCE中,∠ABC=120°,BC=2CD,AD=AF,AF⊥平面ABCD.
如图,三棱柱ABF-DCE中,∠ABC=120°,BC=2CD,AD=AF,AF⊥平面ABCD.