题目内容
12.执行如图所示的程序框图,则输出的结果为( )
| A. | 12 | B. | 11 | C. | 10 | D. | 9 |
分析 根据程序框图,依次计算运行的结果,直到满足条件T>2016,即可得到n的值.
解答 解:模拟程序的运行,可得
n=2,x=2,y=2,s=4,T=4,执行循环体,
n=3,x=4,y=4,s=8,T=12,
执行循环体,n=4,x=8,y=6,s=14,T=26,
执行循环体,n=5,x=16,y=8,s=24,T=50,
执行循环体,n=6,x=32,y=10,s=42,T=92,
执行循环体,n=7,x=64,y=12,s=76,T=168,
执行循环体,n=8,x=128,y=14,s=142,T=310,
执行循环体,n=9,x=256,y=16,s=272,T=582,
执行循环体,n=10,x=512,y=18,s=530,T=1112,
执行循环体,n=11,x=1024,y=20,s=1044,T=2156,
满足条件T>2016,退出循环,输出n的值为11.
故选:B.
点评 本题考查了循环结构的程序框图,根据框图的流程依次计算程序运行的结果是解答此类问题的常用方法,属于基础题.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
2.函数f(x)=x3-3x2-7x+a的图象与直线y=2x+1相切,则a=( )
| A. | 28或4 | B. | 28或-4 | C. | -28或4 | D. | -28或-4 |
20.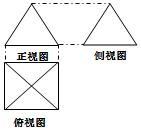 如果一个几何体的三视图如图所示,正视图与侧视图是边长为2的正三角形、俯视图轮廓为正方形,(单位长度:cm),则此几何体的侧面积是( )
如果一个几何体的三视图如图所示,正视图与侧视图是边长为2的正三角形、俯视图轮廓为正方形,(单位长度:cm),则此几何体的侧面积是( )
 如果一个几何体的三视图如图所示,正视图与侧视图是边长为2的正三角形、俯视图轮廓为正方形,(单位长度:cm),则此几何体的侧面积是( )
如果一个几何体的三视图如图所示,正视图与侧视图是边长为2的正三角形、俯视图轮廓为正方形,(单位长度:cm),则此几何体的侧面积是( )| A. | .$2\sqrt{3}$cm | B. | .$4\sqrt{3}$cm2 | C. | 8 cm2 | D. | 12 cm2 |
17.某电脑公司有6名产品推销员,其工作年限与年推销金额的数据如表:
(1)以工作年限为自变量,推销金额为因变量y,作出散点图;
(2)求年推销金额y关于工作年限x的线性回归方程;
(3)若第6名推销员的工作年限为11年,试估计他的年推销金额.
附:回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$中,$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{5}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{5}({x}_{i}-\overline{x})^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.
| 推销员编号 | 1 | 2 | 3 | 4 | 5 |
| 工作年限x/年 | 3 | 5 | 6 | 7 | 9 |
| 推销金额y/万元 | 2 | 3 | 3 | 4 | 5 |
(2)求年推销金额y关于工作年限x的线性回归方程;
(3)若第6名推销员的工作年限为11年,试估计他的年推销金额.
附:回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$中,$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{5}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{5}({x}_{i}-\overline{x})^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.
1.已知半径为r的圆内切于某等边三角形,若在该三角形内任取一点,则该点到圆心的距离大于半径r的概率为( )
| A. | $\frac{\sqrt{3}π}{9}$ | B. | 1-$\frac{\sqrt{3}π}{9}$ | C. | $\frac{\sqrt{3}π}{18}$ | D. | 1-$\frac{\sqrt{3}π}{18}$ |

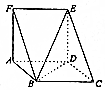 如图,三棱柱ABF-DCE中,∠ABC=120°,BC=2CD,AD=AF,AF⊥平面ABCD.
如图,三棱柱ABF-DCE中,∠ABC=120°,BC=2CD,AD=AF,AF⊥平面ABCD.