题目内容
11.对于两条不同的直线m,n和两个不同的平面α,β,以下结论正确的是( )| A. | 若m?α,n∥β,m,n是异面直线,则α,β相交 | |
| B. | 若m⊥α,m⊥β,n∥α,则n∥β | |
| C. | 若m?α,n∥α,m,n共面于β,则m∥n | |
| D. | 若m⊥α,n⊥β,α,β不平行,则m,n为异面直线 |
分析 根据空间直线和平面平行或垂直的判定定理和性质定理分别进行判断即可.
解答 解:A.α∥β时,m?α,n∥β,m,n是异面直线,可以成立,故A错误,
B.若m⊥α,m⊥β,则α∥β,因为n∥α,则n∥β或n?β,故B错误,
C.利用线面平行的性质定理,可得C正确,
D.若m⊥α,n⊥β,α,β不平行,则m,n为异面直线或相交直线,故D不正确,
故选:C.
点评 本题主要考查与空间直线和平面位置关系的判断,要求熟练掌握相应的判定定理和性质定理.

练习册系列答案
相关题目
1.已知半径为r的圆内切于某等边三角形,若在该三角形内任取一点,则该点到圆心的距离大于半径r的概率为( )
| A. | $\frac{\sqrt{3}π}{9}$ | B. | 1-$\frac{\sqrt{3}π}{9}$ | C. | $\frac{\sqrt{3}π}{18}$ | D. | 1-$\frac{\sqrt{3}π}{18}$ |
6. 某三棱锥的三视图如图所示,则该三棱锥的各个侧面中最大的侧面的面积为( )
某三棱锥的三视图如图所示,则该三棱锥的各个侧面中最大的侧面的面积为( )
 某三棱锥的三视图如图所示,则该三棱锥的各个侧面中最大的侧面的面积为( )
某三棱锥的三视图如图所示,则该三棱锥的各个侧面中最大的侧面的面积为( )| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{5}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\sqrt{2}$ |
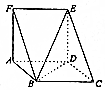 如图,三棱柱ABF-DCE中,∠ABC=120°,BC=2CD,AD=AF,AF⊥平面ABCD.
如图,三棱柱ABF-DCE中,∠ABC=120°,BC=2CD,AD=AF,AF⊥平面ABCD. 共享单车是指由企业在校园、公交站点、商业区、公共服务区等场所提供的自行车单车共享服务,由于其依托“互联网+”,符合“低碳出行”的理念,已越来越多地引起了人们的关注.某部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照[50,60),[60,70),…,[90,100]分成5组,制成如图所示频率分直方图.
共享单车是指由企业在校园、公交站点、商业区、公共服务区等场所提供的自行车单车共享服务,由于其依托“互联网+”,符合“低碳出行”的理念,已越来越多地引起了人们的关注.某部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照[50,60),[60,70),…,[90,100]分成5组,制成如图所示频率分直方图.