题目内容
设数列{an}满足an+1=2nan-an2+2,a1=1,n∈N*,求a2,a3,a4及an.
考点:数学归纳法,数列递推式
专题:点列、递归数列与数学归纳法
分析:根据数列的递推公式直接进行求解,然后利用数学归纳法进行证明即可得到结论.
解答:
解:∵an+1=2nan-an2+2,
∴a2=2a1-a12+2、2-1+2=3,
a3=4a2-a22+2=12-9+2=5,
a4=6a3-a32+2=30-25+2=7,
故猜想an=2n-1,
证明:当n=1,a1=2-1=1,命题成立,
若n=k,命题成立,即ak=2k-1,
则当n=k+1时,ak+1=2kak-ak2+2=2k(2k-1)-(2k-1)2+2=4k2-2k-4k2+4k-1+2=2k+1=2(k+1)-1,
故当n=k+1时,命题也成立,
综上对于n∈N•,an=2n-1成立.
∴a2=2a1-a12+2、2-1+2=3,
a3=4a2-a22+2=12-9+2=5,
a4=6a3-a32+2=30-25+2=7,
故猜想an=2n-1,
证明:当n=1,a1=2-1=1,命题成立,
若n=k,命题成立,即ak=2k-1,
则当n=k+1时,ak+1=2kak-ak2+2=2k(2k-1)-(2k-1)2+2=4k2-2k-4k2+4k-1+2=2k+1=2(k+1)-1,
故当n=k+1时,命题也成立,
综上对于n∈N•,an=2n-1成立.
点评:本题主要考查数列的递推公式的应用,根据数学归纳法是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
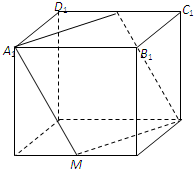 在棱长为a的正方体ABCD-A1B1C1D1中,M是棱AB的中点,过A1,M,C三点的平面交棱C1D1于N点,
在棱长为a的正方体ABCD-A1B1C1D1中,M是棱AB的中点,过A1,M,C三点的平面交棱C1D1于N点,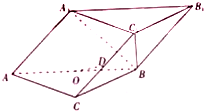 三棱柱ABC-A1B1C1中,平面A1ABB1⊥平面ABC,O是AB的中点.
三棱柱ABC-A1B1C1中,平面A1ABB1⊥平面ABC,O是AB的中点.