题目内容
已知半圆O的直径AB=2,C在BA的延长线上且AC=1,P为半圆上异于A、B的一点,设∠POC=θ.
(1)设PB2+PC2=f(θ),求f(θ)的解析式;
(2)以PC为边作正方形PCMN,求五边形OCMNP面积的最大值.
(1)设PB2+PC2=f(θ),求f(θ)的解析式;
(2)以PC为边作正方形PCMN,求五边形OCMNP面积的最大值.
考点:直线和圆的方程的应用
专题:圆锥曲线的定义、性质与方程
分析:(1)PC2=PO2+CO2-2×PO×CO×cosθ=5-4×cosθ,PB2=PO2+BO2-2×PO×BO×cos(180°-θ)=2+2×cosθ,由此能求出f(θ).
(2)设五边形OCMNP的面积为S,由S=PC2+
PO×CO×sinθ=5-4cosθ+sinθ,能求出五边形OCMNP面积的最大值.
(2)设五边形OCMNP的面积为S,由S=PC2+
| 1 |
| 2 |
解答:
解:(1)∵PC2=PO2+CO2-2×PO×CO×cosθ
=5-4×cosθ,
PB2=PO2+BO2-2×PO×BO×cos(180°-θ)
=2+2×cosθ,
∴f(θ)=7-2cosθ(0°<θ<180°).
(2)设五边形OCMNP的面积为S,
S=PC2+
PO×CO×sinθ
=5-4cosθ+sinθ
=5+
×sin(θ-α),(tanα=4,0°≤θ<180°),
∴Smax=5+
.
=5-4×cosθ,
PB2=PO2+BO2-2×PO×BO×cos(180°-θ)
=2+2×cosθ,
∴f(θ)=7-2cosθ(0°<θ<180°).
(2)设五边形OCMNP的面积为S,
S=PC2+
| 1 |
| 2 |
=5-4cosθ+sinθ
=5+
| 17 |
∴Smax=5+
| 17 |
点评:本题考查函数的解析式的求法,考查五边形面积的最大值的求法,解题时要认真审题,注意三角函数的合理运用.

练习册系列答案
相关题目
在平行四边形ABCD中,
+
-
等于( )
| BC |
| CD |
| AD |
A、
| ||
B、
| ||
C、
| ||
D、
|
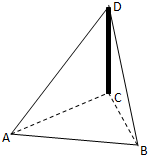 如图所示,哈三中甲,乙两位同学分别站在新校区体育场内的A,B两点,利用三角函数知识测量锅炉房烟囱CD的高.已知AB=15米,∠DAC=60°,∠CAB=15°,∠CBA=45°,求烟囱CD的高.
如图所示,哈三中甲,乙两位同学分别站在新校区体育场内的A,B两点,利用三角函数知识测量锅炉房烟囱CD的高.已知AB=15米,∠DAC=60°,∠CAB=15°,∠CBA=45°,求烟囱CD的高.