题目内容
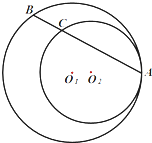如图，圆O1与圆O2内切于点A，其半径分别为r1与r2（r1＞r2），圆O1的弦AB交圆O2于点C（O1不在AB上），求证：AB：AC为定值．考点：与圆有关的比例线段
专题：选作题,立体几何
分析：根据⊙O1与⊙O2内切于点A，可以得出O1，O2，A，在一条直线上，作O1F⊥AB，O2E⊥AB于点F，E，利用平行线分线段成比例定理性质以及垂径定理得出即可．
解答：
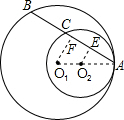证明：根据⊙O1与⊙O2内切于点A，可以得出O1，O2，A，在一条直线上，连接O1，O2，A，分别过点O1，O2作O1F⊥AB，O2E⊥AB于点F，E，
∵O1F⊥AB，O2E⊥AB，
∴AE=CE，AC=BF，
∴
=
，
∵O1F⊥AB，O2E⊥AB，
∴O1F∥O2E，
∴
=
=
，
∴
=
是定值．
证明：根据⊙O1与⊙O2内切于点A，可以得出O1，O2，A，在一条直线上，连接O1，O2，A，分别过点O1，O2作O1F⊥AB，O2E⊥AB于点F，E，∵O1F⊥AB，O2E⊥AB，
∴AE=CE，AC=BF，
∴
| AB |
| AC |
| AF |
| AE |
∵O1F⊥AB，O2E⊥AB，
∴O1F∥O2E，
∴
| AF |
| AE |
| AO1 |
| AO2 |
| r1 |
| r2 |
∴
| AB |
| AC |
| r1 |
| r2 |
点评：此题主要考查了相切两圆的性质以及垂径定理和平行线分线段成比例定理性质，根据已知得出
=
是解题关键．
| AF |
| AE |
| AO1 |
| AO2 |
练习册系列答案
相关题目
随机抽取某中学甲乙两个班各10名同学，测得他们的身高（单位：cm）获得身高数据的茎叶图，如图所示：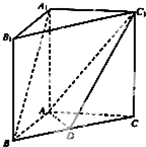
如图，在直三棱柱ABC-A1B1C1中，点D是BC的中点．
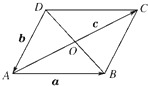如图所示，O是平行四边形ABCD的对角线AC，BD的交点，设