题目内容
已知椭圆的焦点是F1(-1,0),F2(1,0),P为椭圆上一点,且|F1F2|是|PF1|和|PF2|的等差中项,若点P在第三象限,且∠PF1F2=120°,求tan∠F1PF2的值.
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:设|PF1|=m,|PF2|=n,利用F1F2|是|PF1|,|PF2|的等差中项及余弦定理,正弦定理可求tan∠F1PF2的值.
解答:
解:设|PF1|=m,|PF2|=n,则
解方程组,得m=
,n=
.
由正弦定理,得
=
,
∴sin∠F1PF2=
,
∴tan∠F1PF2=
.
|
解方程组,得m=
| 6 |
| 5 |
| 14 |
| 5 |
由正弦定理,得
| 2 |
| sin∠F1PF2 |
| ||
| sin∠PF1F2 |
∴sin∠F1PF2=
5
| ||
| 14 |
∴tan∠F1PF2=
5
| ||
| 11 |
点评:本题主要考查椭圆的性质,考查等差中项及余弦定理,正弦定理,比较基础.

练习册系列答案
相关题目
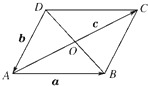 如图所示,O是平行四边形ABCD的对角线AC,BD的交点,设
如图所示,O是平行四边形ABCD的对角线AC,BD的交点,设