题目内容
1．设函数$f（x）=|{x+b}|+|{x-\frac{1}{b}}|（b＞0）$，则函数f（x）能取得（ ）| A． | 最小值为2 | B． | 最大值为2 | C． | 最小值为-2 | D． | 最大值为-2 |
分析 由题，结合绝对值的几何意义可知当x对应的点位于-b及$\frac{1}{b}$对应点之间（含端点）时f（x）最小，进而利用基本不等式可得结论．
解答 解：由题意可知b＞0，由绝对值的几何意义可知
f（x）表示数轴上x对应的点与-b及$\frac{1}{b}$对应点的距离之和，
显然f（x）无最大值，但有最小值，
即当x对应的点位于-b及$\frac{1}{b}$对应点之间（含端点）时，f（x）最小，
此时f（x）min=$\frac{1}{b}$+b≥2$\sqrt{\frac{1}{b}×b}$=2，当且仅当b=1时取等号，
故选：A．
点评 本题考查绝对值函数，考查绝对值的几何意义，考查基本不等式，注意解题方法的积累，属于中档题．
练习册系列答案
相关题目
9．
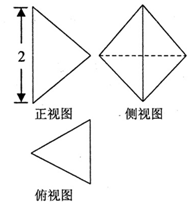某几何体的三视图如图所示，其俯视图是边长为1的正三角形，侧视图是菱形，则这个几何体的体积为（ ）
某几何体的三视图如图所示，其俯视图是边长为1的正三角形，侧视图是菱形，则这个几何体的体积为（ ）| A． | $\frac{\sqrt{3}}{2}$ | B． | $\frac{\sqrt{3}}{6}$ | C． | $\frac{1}{2}$ | D． | $\sqrt{3}$ |