题目内容
13.已知O为坐标原点,圆M:x2+y2-2x-15=0,定点F(-1,0),点N是圆M上一动点,线段NF的垂直平分线交圆M的半径MN于点Q,点Q的轨迹为C.(Ⅰ)求曲线C的方程;
(Ⅱ)不垂直于x轴且不过F点的直线l与曲线C相交于A,B两点,若直线FA、FB的斜率之和为0,则动直线l是否一定经过一定点?若过一定点,则求出该定点的坐标;若不过定点,请说明理由.
分析 (Ⅰ)推导出动点Q的轨迹为以M、F为焦点、长轴长为4的椭圆,由此能求出曲线C的方程.
(Ⅱ)设直线l的方程为y=kx+m,A(x1,y1),B(x2,y2),联立$\left\{\begin{array}{l}{y=kx+m}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,得(3+4k2)x2+8kmx+4m2-12=0,由此利用韦达定理、直线斜率公式求出m=4k,从而直线l的方程为y=kx+4k=k(x+4),由此得到直线l过定点(-4,0).
解答 解:(Ⅰ)由题意知|MQ|+|FQ|=|MN|=4,
又|MF|=2<4,
∴由椭圆定义知动点Q的轨迹为以M、F为焦点、长轴长为4的椭圆,
故2a=4,2c=2,
∴曲线C的方程是$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$.
(Ⅱ)设直线l的方程为y=kx+m,A(x1,y1),B(x2,y2),
联立$\left\{\begin{array}{l}{y=kx+m}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,得(3+4k2)x2+8kmx+4m2-12=0,
则${x}_{1}+{x}_{2}=\frac{-8km}{3+4{k}^{2}}$,${x}_{1}{x}_{2}=\frac{4{m}^{2}-12}{3+4{k}^{2}}$,
由已知,直线FA、FB的斜率之和为:
$\frac{{y}_{1}}{{x}_{1}+1}+\frac{{y}_{2}}{{x}_{2}+1}$=$\frac{k{x}_{1}+m}{{x}_{1}+1}+\frac{k{x}_{2}+m}{{x}_{2}+1}$=$\frac{2k{x}_{1}{x}_{2}+(k+m)({x}_{1}+{x}_{2})+2m}{{x}_{1}{x}_{2}+{x}_{1}+{x}_{2}+1}$=0,
∴2kx1x2+(k+m)(x1+x2)+2m=0,
将${x}_{1}+{x}_{2}=\frac{-8km}{3+4{k}^{2}}$,${x}_{1}{x}_{2}=\frac{4{m}^{2}-12}{3+4{k}^{2}}$代入,得:
$2k•\frac{4{m}^{2}-12}{3+4{k}^{2}}+(k+m)•\frac{-8km}{3+4{k}^{2}}$+2m=0,
化简,得-4k+m=0,即m=4k,
∴直线l的方程为y=kx+4k=k(x+4),
∴直线l过定点(-4,0).
点评 本题考查曲线方程的求法,考查直线是否过定点的判断与求法,涉及到椭圆、直线方程、圆、斜率公式等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.

 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案| A. | sin(α+β)<sinα+sinβ | B. | sin(α+β)>sinα+sinβ | ||
| C. | cos(α+β)<sinα+sinβ | D. | cos(α+β)>cosα+cosβ |
| A. | 最小值为2 | B. | 最大值为2 | C. | 最小值为-2 | D. | 最大值为-2 |
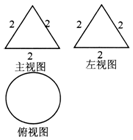
| A. | 3:4 | B. | 3:8 | C. | 3:16 | D. | 9:16 |
| A. | (-$\frac{\sqrt{2}}{4}$,$\frac{\sqrt{2}}{4}$) | B. | (-$\sqrt{3}$,$\sqrt{3}$) | C. | ($-\frac{{\sqrt{3}}}{3},\frac{{\sqrt{3}}}{3})$ | D. | ($-\sqrt{2},-\sqrt{2}$) |
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
 如图是4为评委给某作品打出的分数的茎叶图,那么4为评委打出的分数的方差是$\frac{5}{2}$.
如图是4为评委给某作品打出的分数的茎叶图,那么4为评委打出的分数的方差是$\frac{5}{2}$.