题目内容

12．已知等差数列{an}中，a2=5，前4项和S4=28．
（1）求数列{an}的通项公式；
（2）求数列{an}的前n项和Sn．

分析 （1）利用等差数列的通项公式与求和公式即可得出．
（2）利用等差数列的求和公式即可得出．

解答 解：（1）设等差数列{an}的公差为d，则由已知条件得$\left\{\begin{array}{l}{a_2}={a_1}+d=5\\{S_4}=4{a_1}+\frac{4×3}{2}×d=28\end{array}\right.$（2分）
∴$\left\{\begin{array}{l}{a_1}=1\\ d=4\end{array}\right.$（4分）
∴an=a1+（n-1）×d=4n-3（6分）
（2）由（1）可得${S_n}=n{a_1}+\frac{{n（{n-1}）}}{2}d=2{n^2}-n$（12分）

点评 本题考查了等差数列的通项公式与求和公式，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
2．一个几何体的三视图如图所示，其中俯视图为正方形，则最长侧棱（不包括底面的棱）的长度为（　　）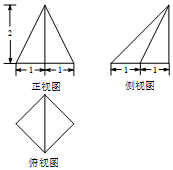
A．2B．$\sqrt{6}$C．$2\sqrt{2}$D．$2\sqrt{3}$
3．已知$α，β∈（0，\frac{π}{2}）$，则下列不等式一定成立的是（　　）
A．sin（α+β）＜sinα+sinβB．sin（α+β）＞sinα+sinβ
C．cos（α+β）＜sinα+sinβD．cos（α+β）＞cosα+cosβ
20．函数$f（x）=\sqrt{x+1}+lg（x-3）$的定义域是（　　）
A．[-1，3）B．（-∞，-1]C．[3，+∞）D．（3，+∞）
7．已知极坐标的极点在平面直角坐标系的原点O处，极轴与x轴的非负半轴重合，且长度单位相同．直线的极坐标方程为ρsin（θ-$\frac{π}{3}$）=$\sqrt{3}$，若点P为曲线C：$\left\{\begin{array}{l}x=2+2cosα\\ y=2sinα\end{array}\right.$，
（α为参数）上的动点．
（1）试写直线的直角坐标方程及曲线C的普通方程；
（2）求点P到直线距离的最大值．
17．已知不等式ax2-bx-1≥0的解是[-$\frac{1}{2}$，-$\frac{1}{3}$]
（1）求a，b的值；
（2）求不等式x2-bx-a＜0的解集．
4．在直角坐标系xOy中，曲线${C_1}：\left\{{\begin{array}{l}{x=tcosα}\\{y=tsinα}\end{array}}\right.$（t为参数，t≠0），其中0≤a＜π，在以O为极点，x轴正半轴为极轴的极坐标系中，曲线C2：ρ=4sinθ，曲线${C_3}=ρ=4\sqrt{3}cosθ$．
（Ⅰ）求C2与C3交点的直角坐标系；
（Ⅱ）若C2与C1相交于点A，C3与C1相交于点B，求|AB|的最大值．
1．设函数$f（x）=|{x+b}|+|{x-\frac{1}{b}}|（b＞0）$，则函数f（x）能取得（　　）
A．最小值为2B．最大值为2C．最小值为-2D．最大值为-2
2．如图是4为评委给某作品打出的分数的茎叶图，那么4为评委打出的分数的方差是$\frac{5}{2}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网