题目内容
在等比数例{an}中,2a4,a6,48成等差数列,且a3•a5=64,则{an}的前8项和为( )
| A、255 | B、85 |
| C、255或-85 | D、255或85 |
考点:等差数列与等比数列的综合
专题:等差数列与等比数列
分析:利用等比数列的性质求出a4,然后求出a6,求出公比,即可求解{an}的前8项和.
解答:
解:在等比数例{an}中,a3•a5=64,可得a42=64,解得a4=±8.
当a4=8时,2a4,a6,48成等差数列,即16,a6,48成等差数列,可得a6=32.
q2=
=4,解得q=±2,q=2时解得a1=
=1,q=-2时,q=-1
q=2,a1=1时,S8=
=
=255.
q=-2时解得a1=-1,S8=
=
=85.
当a4=-8时,2a4,a6,48成等差数列,即-16,a6,48成等差数列,可得a6=16.
q2=
无解.
故选:D.
当a4=8时,2a4,a6,48成等差数列,即16,a6,48成等差数列,可得a6=32.
q2=
| 32 |
| 8 |
| a4 |
| q3 |
q=2,a1=1时,S8=
| a1(1-q8) |
| 1-q |
| 1(1-28) |
| 1-2 |
q=-2时解得a1=-1,S8=
| a1(1-q8) |
| 1-q |
| -1(1-(-2)8) |
| 1+2 |
当a4=-8时,2a4,a6,48成等差数列,即-16,a6,48成等差数列,可得a6=16.
q2=
| 16 |
| -8 |
故选:D.
点评:本题考查等差数列以及等比数列的综合应用,考查计算能力.

练习册系列答案
相关题目
已知i是虚数单位,复数z=
,则|z-2|=( )
| 2i |
| 1+i |
| A、2 | ||
B、2
| ||
C、
| ||
| D、1 |
数列0,
,
,
,
,…的通项公式为( )
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 5 |
| 2 |
| 3 |
A、an=
| ||
B、an=
| ||
C、an=
| ||
D、an=
|
 阅读如图所示的程序框图,运行相应的程序.若输出的结果为
阅读如图所示的程序框图,运行相应的程序.若输出的结果为| 1 |
| 2 |
| A、n>3? | B、n<3? |
| C、n<4? | D、n>4? |
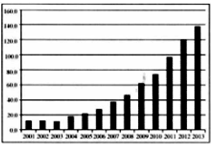 2001年至2013年北京市电影放映场次的情况如图所示.下列函数模型中,最不合适近似描述这13年间电影放映场次逐年变化规律的是( )
2001年至2013年北京市电影放映场次的情况如图所示.下列函数模型中,最不合适近似描述这13年间电影放映场次逐年变化规律的是( )| A、y=ax2+bx+c |
| B、y=aex+b |
| C、y=eax+b |
| D、y=alnx+b |
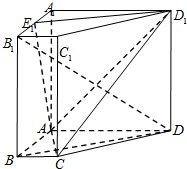 如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面 ABCD,底面ABCD是直角梯形,AD∥BC,∠BAD=90°,AD=AA1=3,BC=1,E1为A1B1中点.
如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面 ABCD,底面ABCD是直角梯形,AD∥BC,∠BAD=90°,AD=AA1=3,BC=1,E1为A1B1中点. 如图,已知椭圆C:
如图,已知椭圆C: