题目内容
某学习小组共有A,B,C,D四位同学,他们的身高(单位:米)及体重指标(单位:千克/米2)
如下表所示:
(1)求这四位同学体重指标的中位数.
(2)从该小组身高低于1.80的同学中任选2人,求选到的2人身高都在1.75以下的概率.
如下表所示:
| A | B | C | D | |
| 身高 | 1.69 | 1.73 | 1.75 | 1.80 |
| 体重指标 | 19.2 | 25.0 | 18.5 | 24.8 |
(2)从该小组身高低于1.80的同学中任选2人,求选到的2人身高都在1.75以下的概率.
考点:列举法计算基本事件数及事件发生的概率,众数、中位数、平均数
专题:概率与统计
分析:(1)根据中位数的概念即可得到结果;
(2)列出一切可能的结果,挑出满足条件的情况即可得到结论.
(2)列出一切可能的结果,挑出满足条件的情况即可得到结论.
解答:
解:(1)这四位同学体重指标的中位数为
=22.
(2)从身高低于1.80的同学中任选2人,
其一切可能的结果组成的基本事件有:
(A,B),(A,C),(B,C),共3个.
由于每个人被选到的机会均等,因此这些基本事件的出现是等可能的.
选到的2人身高都在1.75以下的事件有:(A,B)共1个,因此P=
,
故选到的2人身高都在1.78以下的概率为
.
| 19.2+24.8 |
| 2 |
(2)从身高低于1.80的同学中任选2人,
其一切可能的结果组成的基本事件有:
(A,B),(A,C),(B,C),共3个.
由于每个人被选到的机会均等,因此这些基本事件的出现是等可能的.
选到的2人身高都在1.75以下的事件有:(A,B)共1个,因此P=
| 1 |
| 3 |
故选到的2人身高都在1.78以下的概率为
| 1 |
| 3 |
点评:本题考查中位数及古典概型,属基础题.

练习册系列答案
相关题目
若非零实数a,b,c成等差数列,则函数y=ax2+bx+
c的图象与x轴交点的个数为( )
| 1 |
| 4 |
| A、0 | B、1 | C、2 | D、1或2 |
数列0,
,
,
,
,…的通项公式为( )
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 5 |
| 2 |
| 3 |
A、an=
| ||
B、an=
| ||
C、an=
| ||
D、an=
|
 阅读如图所示的程序框图,运行相应的程序.若输出的结果为
阅读如图所示的程序框图,运行相应的程序.若输出的结果为| 1 |
| 2 |
| A、n>3? | B、n<3? |
| C、n<4? | D、n>4? |
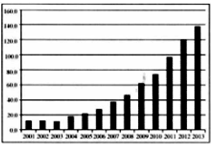 2001年至2013年北京市电影放映场次的情况如图所示.下列函数模型中,最不合适近似描述这13年间电影放映场次逐年变化规律的是( )
2001年至2013年北京市电影放映场次的情况如图所示.下列函数模型中,最不合适近似描述这13年间电影放映场次逐年变化规律的是( )| A、y=ax2+bx+c |
| B、y=aex+b |
| C、y=eax+b |
| D、y=alnx+b |
已知凼数F(x)为二次凼数,且F(x)的导凼数为f(x),若存在实数a∈(-2,-1),使f(-a)=-f(a)>0,则不等式F(2x-1)>F(x)的解集为( )
A、{x|x<
| ||
B、{x|x<
| ||
C、{x|
| ||
D、{x|x<-1或x>-
|
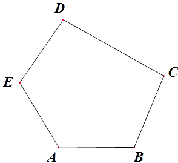 如图所示,一个确定的凸五边形 ABCDE,令x=
如图所示,一个确定的凸五边形 ABCDE,令x=