题目内容
设a，b为不相等的实数，求证：（a4+b4）（a2+b2）＞（a3+b3）2．
考点：不等式的证明
专题：证明题,推理和证明
分析：根据柯西不等式，有（a4+b4）（a2+b2）≥（a2•a+b2•b）2=（a3+b3）2．结合a，b为不相等的实数，即可证明结论．
解答：
证明：根据柯西不等式，有（a4+b4）（a2+b2）≥（a2•a+b2•b）2=（a3+b3）2．
∴（a4+b4）（a2+b2）≥（a3+b3）2．
∵a，b为不相等的实数，
∴（a4+b4）（a2+b2）＞（a3+b3）2．
∴（a4+b4）（a2+b2）≥（a3+b3）2．
∵a，b为不相等的实数，
∴（a4+b4）（a2+b2）＞（a3+b3）2．
点评：本题考查不等式的证明，考查柯西不等式，比较基础．
练习册系列答案
相关题目
已知复数z=
，则|z|=（ ）
1+
| ||
| 1-i |
| A、1 | ||
B、
| ||
| C、2 | ||
| D、4 |
下列4个正方体图形中，l是正方体的一条对角线，点M、N、P分别为其所在棱的中点，能得出直线l⊥面MNP的所有图形的序号是（ ）
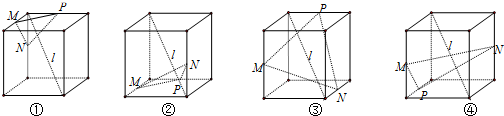
| A、①④ | B、①② | C、②④ | D、①③ |
数列0，
，
，
，
，…的通项公式为（ ）
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 5 |
| 2 |
| 3 |
A、an=
| ||
B、an=
| ||
C、an=
| ||
D、an=
|
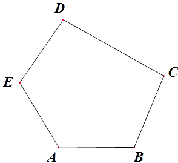如图所示，一个确定的凸五边形 ABCDE，令x=