题目内容
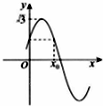已知f（x）=Asin（2x+| π |
| 6 |
（Ⅰ）写出f（x）的最小正周期及 A，x0的值；
（Ⅱ）求f（x）在（-
| π |
| 4 |
| π |
| 3 |
考点：正弦函数的图象
专题：三角函数的图像与性质
分析：（Ⅰ）根据f（x）的部分图象，可得A 和T．令2x+
=
，求得x=
，求得f（x）位于y轴右侧的第一条对称轴方程为x=
，可得x0的值．
（Ⅱ）由x∈（-
，
），利用正弦函数的定义域和值域，求得f（x）在（-
，
）上的取值范围．
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
（Ⅱ）由x∈（-
| π |
| 4 |
| π |
| 3 |
| π |
| 4 |
| π |
| 3 |
解答：
解：（Ⅰ）根据f（x）=Asin（2x+
）（ A＞0）的部分图象，可得A=
，T=
=π，
令2x+
=
，求得x=
，故f（x）位于y轴右侧的第一条对称轴方程为x=
，∴x0=2×
=
．
（Ⅱ）由x∈（-
，
），可得2x+
∈（-
，
），sin（2x+
）∈（-
，1]，
故
sin（2x+
）∈（-
，
]．
| π |
| 6 |
| 3 |
| 2π |
| 2 |
令2x+
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
（Ⅱ）由x∈（-
| π |
| 4 |
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
| 5π |
| 6 |
| π |
| 6 |
| ||
| 2 |
故
| 3 |
| π |
| 6 |
| 3 |
| 2 |
| 3 |
点评：本题主要考查正弦函数的图象和性质，正弦函数的定义域和值域，属于基础题．
练习册系列答案
53天天练系列答案
相关题目
下列4个正方体图形中，l是正方体的一条对角线，点M、N、P分别为其所在棱的中点，能得出直线l⊥面MNP的所有图形的序号是（ ）
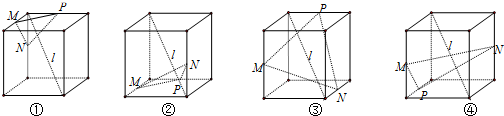
| A、①④ | B、①② | C、②④ | D、①③ |
数列0，
，
，
，
，…的通项公式为（ ）
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 5 |
| 2 |
| 3 |
A、an=
| ||
B、an=
| ||
C、an=
| ||
D、an=
|
阅读如图所示的程序框图，运行相应的程序．若输出的结果为| 1 |
| 2 |
| A、n＞3？ | B、n＜3？ |
| C、n＜4？ | D、n＞4？ |
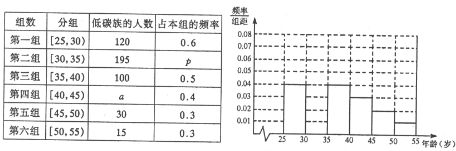
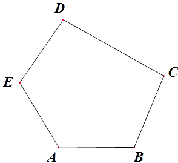如图所示，一个确定的凸五边形 ABCDE，令x=