题目内容
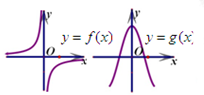
函数y=f(x)与y=g(x)的图象如图,则函数y=f(x)•g(x)的图象可能是( )

A、 |
B、 |
C、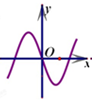 |
D、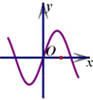 |
考点:函数的图象
专题:函数的性质及应用
分析:观察函数y=f(x)的图象得出函数在x=0无意义,故函数y=f(x)•g(x)在x=0无意义,可排除CD;
令x再取很小的正数,从图象可得f(x)<0,g(x)>0,可得A适合而B不适合,可得答案.
令x再取很小的正数,从图象可得f(x)<0,g(x)>0,可得A适合而B不适合,可得答案.
解答:
解:∵函数y=f(x)在x=0无意义,∴函数y=f(x)•g(x)在x=0无意义,∴排除CD;
当x是很小的正数时,从图象可得f(x)<0,g(x)>0,∴f(x)•g(x)<0,故A适合而B不适合,
故选:A.
当x是很小的正数时,从图象可得f(x)<0,g(x)>0,∴f(x)•g(x)<0,故A适合而B不适合,
故选:A.
点评:本题主要考查函数的图象的应用,解题的关键是:要从所给的函数图象得出函数成立的信息,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知命题p:,a2≥0(a∈R),命题q:sinα=sinβ是α=β的充分条件,则下列命题中为真命题的是( )
| A、p∧q |
| B、p∨q |
| C、(¬p)∧(¬q) |
| D、(¬p)∨q |
集合﹛(x,y)|xy<0,x∈R,y∈R﹜是指( )
| A、第一、三象限内所有的点的集合 |
| B、第二、四象限内所有的点的集合 |
| C、不在第一、三象限内所有的点的集合 |
| D、不在第二、四象限内所有的点的集合 |
直线Ax+By+C=0通过第二、三、四象限,则系数A,B,C需满足条件( )
| A、C=0,AB<0 |
| B、AC<0,BC<0 |
| C、A,B,C同号 |
| D、A=0,BC<0 |
已知二次函数的图象如图所示,则其导函数f′(x)的图象大致形状是( )


A、 |
B、 |
C、 |
D、 |
若实数x,y满足x+y+(x-y)i=2,则xy的值是( )
| A、1 | B、2 | C、-2 | D、-3 |