题目内容
已知关于x的不等式x2-3x+m<0是{x|1<x<n}(n>1).
(1)求实数m,n的值;
(2)若正数a,b满足:ma+2nb=1,求a-b的最大值.
(1)求实数m,n的值;
(2)若正数a,b满足:ma+2nb=1,求a-b的最大值.
考点:基本不等式,一元二次不等式的解法
专题:不等式的解法及应用
分析:(1)利用根与系数的关系即可得出;
(2)利用基本不等式的性质即可得出.
(2)利用基本不等式的性质即可得出.
解答:
解:(1)由题意可知:1,n是x2-3x+m=0的两根,
∴1+n=3,1×n═m,
∵n>1,
∴m=2,n=2.
(2)把m=2,n=2代入ma+2nb=1,得a+2b=
.
∴2
≤
,
解得:a•b≤
.
当且仅当a=2b=
,即a=
,b=
时等号成立.
∴ab的最大值为
.
∴1+n=3,1×n═m,
∵n>1,
∴m=2,n=2.
(2)把m=2,n=2代入ma+2nb=1,得a+2b=
| 1 |
| 2 |
∴2
| 2ab |
| 1 |
| 2 |
解得:a•b≤
| 1 |
| 32 |
当且仅当a=2b=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 8 |
∴ab的最大值为
| 1 |
| 32 |
点评:利用一元二次方程的根与系数的关系、基本不等式的性质,属于基础题.

练习册系列答案
 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
在直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴建立极坐标系.若极坐标方程为ρcosθ=4的直线与曲线
(t为参数)相交于A,B两点,则|AB|=( )
|
| A、2 | B、4 | C、8 | D、16 |
已知a,b为实数,则“a+b≥2”是“a≥1且b≥1”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
如图是一个算法的程序框图,则输出的结果是( )


A、
| ||
B、
| ||
C、
| ||
D、
|
甲、乙两人在一次赛跑中路程s与t的函数关系如图所示,则下列说法正确的是( )
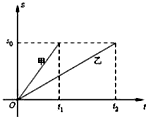

| A、甲比乙先出去 |
| B、乙比甲跑的路程多 |
| C、甲先到达终点 |
| D、甲、乙两人的速度相同 |