题目内容
已知命题p：，a2≥0（a∈R），命题q：sinα=sinβ是α=β的充分条件，则下列命题中为真命题的是（ ）
| A、p∧q |
| B、p∨q |
| C、（￢p）∧（￢q） |
| D、（￢p）∨q |
考点：复合命题的真假
专题：简易逻辑
分析：命题p：，a2≥0（a∈R），是真命题．命题q：sinα=sinβ是α=β的充分不必要条件．即可判断出．
解答：
解：命题p：，a2≥0（a∈R），是真命题．
命题q：sinα=sinβ是α=β的充分不必要条件，因此是假命题．
∴只有p∨q是真命题．
故选：B．
命题q：sinα=sinβ是α=β的充分不必要条件，因此是假命题．
∴只有p∨q是真命题．
故选：B．
点评：本题考查了简易逻辑的判定、实数的性质、三角函数的性质，考查了推理能力与计算能力，属于基础题．
练习册系列答案
黄冈经典趣味课堂系列答案
启东小题作业本系列答案
相关题目
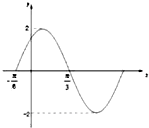
如图是函数f（x）=Asin（ωx+φ）的部分图象，则f（x）的表达式为（ ）
A、f（x）=2sin（2x-
| ||
B、f（x）=2sin（2x+
| ||
C、f（x）=2sin（x+
| ||
D、f（x）=2sin（2x-
|
