题目内容
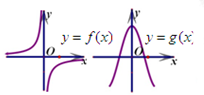
已知二次函数的图象如图所示,则其导函数f′(x)的图象大致形状是( )


A、 |
B、 |
C、 |
D、 |
考点:函数的图象
专题:函数的性质及应用,导数的概念及应用
分析:先根据图象可知二次函数的二次项系数为正,由于对称轴为y轴可知一次项系数为0,然后写出它的导函数即可直接判断.
解答:
解:∵二次函数的图象开口向上,∴二次函数的二次项系数为正,
∵对称轴为y轴
∴一次项系数为0,
设其为y=ax2+c,且a>0,
∴y′=2ax,且a>0,过原点与第一三象限;
故选:C.
∵对称轴为y轴
∴一次项系数为0,
设其为y=ax2+c,且a>0,
∴y′=2ax,且a>0,过原点与第一三象限;
故选:C.
点评:本题考查了根据图象写出函数式的知识和导函数的写法.

练习册系列答案
相关题目
如图是函数f(x)=Asin(ωx+φ)的部分图象,则f(x)的表达式为( )
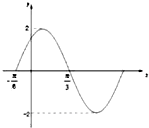

A、f(x)=2sin(2x-
| ||
B、f(x)=2sin(2x+
| ||
C、f(x)=2sin(x+
| ||
D、f(x)=2sin(2x-
|
已知a,b为实数,则“a+b≥2”是“a≥1且b≥1”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
函数y=
-2x的导数是( )
| 2x2+1 |
| x |
A、2-
| ||
B、-
| ||
C、x-
| ||
D、
|
甲、乙两人在一次赛跑中路程s与t的函数关系如图所示,则下列说法正确的是( )
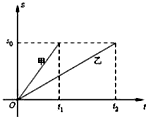

| A、甲比乙先出去 |
| B、乙比甲跑的路程多 |
| C、甲先到达终点 |
| D、甲、乙两人的速度相同 |
已知全集U=R,集合A={x|x<3},B={x|lnx<0},则A∩∁UB( )
| A、{x|1<x<3} |
| B、{x|x≤0或1≤x<3} |
| C、{x|x<3} |
| D、{x|1≤x<3} |