题目内容
已知圆C的圆心与抛物线y2=4x的焦点关于直线y=x对称,又直线4x-3y-2=0与圆C相切,则圆C的标准方程为 .
考点:圆的标准方程
专题:直线与圆
分析:由已知得圆心C(0,1),圆半径r等于圆心C(0,1)到直线4x-3y-2=0的距离.
解答:
解:∵圆C的圆心与抛物线y2=4x的焦点F(1,0)关于直线y=x对称,
∴圆心C(0,1),
又直线4x-3y-2=0与圆C相切,
∴圆半径r等于圆心C(0,1)到直线4x-3y-2=0的距离,
∴r=
=1,
∴圆的标准方程为x2+(y-1)2=1.
故答案为:x2+(y-1)2=1.
∴圆心C(0,1),
又直线4x-3y-2=0与圆C相切,
∴圆半径r等于圆心C(0,1)到直线4x-3y-2=0的距离,
∴r=
| |0-3-2| | ||
|
∴圆的标准方程为x2+(y-1)2=1.
故答案为:x2+(y-1)2=1.
点评:本题考查圆的标准方程的求法,是中档题,解题时要注意抛物线性质和点到直线的距离公式的合理运用.

练习册系列答案
相关题目
如图是一个算法的程序框图,则输出的结果是( )


A、
| ||
B、
| ||
C、
| ||
D、
|
甲、乙两人在一次赛跑中路程s与t的函数关系如图所示,则下列说法正确的是( )
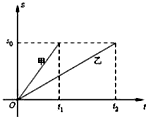

| A、甲比乙先出去 |
| B、乙比甲跑的路程多 |
| C、甲先到达终点 |
| D、甲、乙两人的速度相同 |
由不大于7的质数组成的集合是( )
| A、﹛1,2,3,5,7﹜ |
| B、﹛2,3,5,7﹜ |
| C、﹛2,3,5﹜ |
| D、﹛x|x≤7﹜ |