题目内容
11．已知函数$f（x）=\frac{2}{x}$，则曲线上过点（1，2）处的切线方程为2x+y-4=0．分析 求出f（x）的导数，由导数的几何意义，可得切线的斜率，再由点斜式方程即可得到所求切线的方程．
解答 解：函数$f（x）=\frac{2}{x}$的导数为f′（x）=-$\frac{2}{{x}^{2}}$，
可得在（1，2）处切线的斜率为-2，
曲线上过点（1，2）处的切线方程为y-2=-2（x-1），
即为2x+y-4=0．
故答案为：2x+y-4=0．
点评 本题考查导数的运用：求切线方程，考查导数的几何意义，正确求导和运用点斜式方程是解题的关键，属于基础题．
练习册系列答案
开心蛙状元测试卷系列答案
相关题目
1．
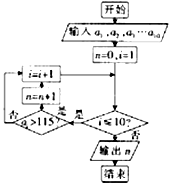某旅游景点统计了今年5月1号至10号每天的门票收入（单位：万元），分别记为a1，a2，…，a10（如：a3表示5月3号的门票收入），表是5月1号到5月10号每天的门票收入，根据表中数据，下面程序框图输出的结果为（ ）
某旅游景点统计了今年5月1号至10号每天的门票收入（单位：万元），分别记为a1，a2，…，a10（如：a3表示5月3号的门票收入），表是5月1号到5月10号每天的门票收入，根据表中数据，下面程序框图输出的结果为（ ）| 日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 门票收入（万元） | 80 | 120 | 110 | 91 | 65 | 77 | 131 | 116 | 55 | 77 |
| A． | 3 | B． | 4 | C． | 5 | D． | 6 |
2．执行下面的程序框图，输出的S的值为（ ）
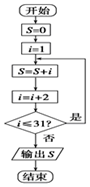
| A． | 225 | B． | 256 | C． | 289 | D． | 324 |
19．下列函数中不是偶函数的是（ ）
| A． | y=sin|x| | B． | y=-|sinx| | C． | y=cosx+1 | D． | y=sin2x |
6．已知tanα=-$\frac{3}{4}，且α∈（\frac{3π}{2}，2π），则cos（\frac{π}{2}+α）的值是$（ ）
| A． | $-\frac{3}{5}$ | B． | $\frac{3}{5}$ | C． | $\frac{4}{5}$ | D． | $-\frac{4}{5}$ |
16．函数$y=2tan（2x-\frac{π}{4}）$的图象的对称中心的坐标是（ ）
| A． | $（\frac{k}{4}π，0），k∈Z$ | B． | $（\frac{k}{2}π，0），k∈Z$ | C． | $（\frac{k}{4}π+\frac{π}{8}，0），k∈Z$ | D． | $（\frac{k}{2}π+\frac{π}{8}，0），k∈Z$ |
3．直角坐标系中，点$（1，-\sqrt{3}）$的极坐标可以是（ ）
| A． | $（2，\frac{5π}{6}）$ | B． | $（2，\frac{11π}{6}）$ | C． | $（2，\frac{4π}{3}）$ | D． | $（2，\frac{5π}{3}）$ |
20．某几何体的三视图如图所示，则其表面积为（ ）
| A． | 18 | B． | 20 | C． | 22 | D． | 24 |
1．已知复数z1=2t+i，z2=1-2i，若$\frac{z_1}{z_2}$为实数，则实数t的值是（ ）
| A． | 1 | B． | -1 | C． | $\frac{1}{4}$ | D． | -$\frac{1}{4}$ |