题目内容
6.已知tanα=-$\frac{3}{4},且α∈(\frac{3π}{2},2π),则cos(\frac{π}{2}+α)的值是$( )| A. | $-\frac{3}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $-\frac{4}{5}$ |
分析 根据tanα求出sinα的值,再利用诱导公式求出cos($\frac{π}{2}$+α)的值.
解答 解:tanα=-$\frac{3}{4}$,
∴$\frac{sinα}{cosα}$=-$\frac{3}{4}$,
∴cosα=-$\frac{4}{3}$sinα,
∴sin2α+cos2α=sin2α+${(-\frac{4}{3}sinα)}^{2}$=$\frac{25}{9}$sin2α=1,
解得sinα=±$\frac{3}{5}$;
又α∈($\frac{3π}{2}$,2π),
∴sinα=-$\frac{3}{5}$,
∴cos($\frac{π}{2}$+α)=-sinα=$\frac{3}{5}$.
故选:B.
点评 本题考查了同角的三角函数关系与诱导公式的应用问题,是基础题.

练习册系列答案
相关题目
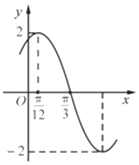 如图为函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$,x∈R)的部分图象.
如图为函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$,x∈R)的部分图象. 如图,在三棱锥A-BCD中,AD⊥平面BCD,CB=CD,AD=DB,P,Q分别在线段AB,AC上,AP=3PB,AQ=2QC,M是BD的中点.
如图,在三棱锥A-BCD中,AD⊥平面BCD,CB=CD,AD=DB,P,Q分别在线段AB,AC上,AP=3PB,AQ=2QC,M是BD的中点.