题目内容
19.下列函数中不是偶函数的是( )| A. | y=sin|x| | B. | y=-|sinx| | C. | y=cosx+1 | D. | y=sin2x |
分析 根据题意,依次分析选项中函数的奇偶性,综合可得答案.
解答 解:根据题意,依次分析选项:
对于A、函数y=sin|x|的定义域为R,f(-x)=sin|-x|=sinx=f(x),为偶函数;
对于B、函数y=-|sinx|的定义域为R,f(-x)=-|sin(-x)|=-|sinx|=f(x),为偶函数;
对于C、函数y=cosx+1的定义域为R,f(-x)=cos(-x)+1=cosx+1=f(x),为偶函数;
对于D、函数y=sin2x=2sinxcosx的定义域为R,f(-x)=2sin(-x)cos(-x)=-2sinxcosx=-f(x),为奇函数;
故选:D.
点评 本题考查函数奇偶性的判定,涉及三角函数的化简计算,关键是理解函数奇偶性的定义.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
9.函数$y=2cos({\frac{1}{2}x+\frac{π}{3}})$图象的一个对称中心为( )
| A. | $({\frac{4π}{3},0})$ | B. | $({\frac{π}{2},0})$ | C. | $({\frac{π}{3},0})$ | D. | $({\frac{π}{6},0})$ |
10.设复数z满足条件|z-(2-2i)|=1,那么z对应的点的轨迹是( )
| A. | 圆 | B. | 椭圆 | C. | 双曲线 | D. | 抛物线 |
8.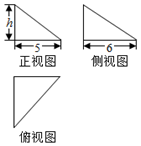 如图所示,三个直角三角形是一个体积为20cm3的几何体的三视图,则该几何体外接球的表面积(单位:cm2)等于( )
如图所示,三个直角三角形是一个体积为20cm3的几何体的三视图,则该几何体外接球的表面积(单位:cm2)等于( )
 如图所示,三个直角三角形是一个体积为20cm3的几何体的三视图,则该几何体外接球的表面积(单位:cm2)等于( )
如图所示,三个直角三角形是一个体积为20cm3的几何体的三视图,则该几何体外接球的表面积(单位:cm2)等于( )| A. | 75π | B. | 77π | C. | 65π | D. | 55π |
9.将函数y=$\sqrt{3}$cosx+sinx(x∈R)的图象向左平移m(m>0)个单位长度后,所得到的图象关于y轴对称,则m的最小值是( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{12}$ | C. | $\frac{π}{6}$ | D. | $\frac{5π}{6}$ |
 如图,在三棱锥A-BCD中,AD⊥平面BCD,CB=CD,AD=DB,P,Q分别在线段AB,AC上,AP=3PB,AQ=2QC,M是BD的中点.
如图,在三棱锥A-BCD中,AD⊥平面BCD,CB=CD,AD=DB,P,Q分别在线段AB,AC上,AP=3PB,AQ=2QC,M是BD的中点.