题目内容
有编号为1,2,3的三个盒子和10个相同的小球,把这10个小球全部装入3个盒子,使得每个盒子所装小球数不小于盒子的编号数,这种装法共有( )
| A、9 | B、12 | C、15 | D、18 |
考点:计数原理的应用
专题:排列组合
分析:首先保证放入和编号相同的球数,只需分析剩下的球的不同方法即可.
解答:
解:先放1,2,3的话,那么还剩下4个球,4个球放到3个不同的盒子里,情况有:
0,0,4,分别在1,2,3号盒子中的任意一个中放4个,共3种情况;
0,1,3,分别在1,2,3号盒子中的任意两个中放3个和1个,共6种情况;
0,2,2,分别在1,2,3号盒子中的任意两个中放2个,共3种情况;
1,1,2分别在1,2,3号盒子中的任意两个中放2个和1个,共3种情况;
∴3+6+3+3=15种.
故选:C.
0,0,4,分别在1,2,3号盒子中的任意一个中放4个,共3种情况;
0,1,3,分别在1,2,3号盒子中的任意两个中放3个和1个,共6种情况;
0,2,2,分别在1,2,3号盒子中的任意两个中放2个,共3种情况;
1,1,2分别在1,2,3号盒子中的任意两个中放2个和1个,共3种情况;
∴3+6+3+3=15种.
故选:C.
点评:本题考查了分类计数原理的应用密切,解题的关键是要注意仔细分析题目,做到分类时不重不漏,属于基础题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
已知函数f(x)=2 x2,它的增区间为( )
| A、(-∞,-1) |
| B、(-∞,0) |
| C、(0,+∞) |
| D、(1,+∞) |
如果在两个平面内分别有一条直线,这两条直线互相平行,那么这两个平面的位置关系一定是( )
| A、平行 | B、相交 |
| C、平行或相交 | D、垂直相交 |
7人站成一排,其中甲不排头,乙不排当中的不同排法种数为( )
| A、4000 | B、3720 |
| C、960 | D、1024 |
“(2x+1)x=0”是“x=0”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
命题“对任意x∈R,都有2x>0”的否定是( )
| A、对任意x∈R,都有2x≤0 |
| B、不存在x∈R,使得2x≤0 |
| C、存在x0∈R,使得2x>0 |
| D、存在x0∈R,2x0≤0 |
已知an=n(n+1),以下四个数中,哪个是数列{an}中的一项( )
| A、18 | B、21 | C、25 | D、30 |
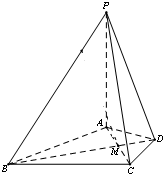 在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=AB=4,∠CDA=120°.
在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=AB=4,∠CDA=120°.