题目内容
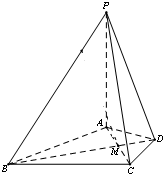在四棱锥P-ABCD中，PA⊥平面ABCD，△ABC是正三角形，AC与BD的交点M恰好是AC中点，又PA=AB=4，∠CDA=120°．（1）求证：BD⊥PC；
（2）求二面角D-PC-B的余弦值．
考点：与二面角有关的立体几何综合题,棱锥的结构特征
专题：
分析：（1）利用线面垂直的判定定理，证明BD⊥平面PAC，可得BD⊥PC；
（2）建立空间直角坐标系，求出平面DPC、平面PBC的法向量，利用向量的夹角公式，即可求二面角D-PC-B的余弦值．
（2）建立空间直角坐标系，求出平面DPC、平面PBC的法向量，利用向量的夹角公式，即可求二面角D-PC-B的余弦值．
解答：
（1）证明：∵△ABC是正三角形，M是AC中点，
∴BM⊥AC，即BD⊥AC．
又∵PA⊥平面ABCD，∴PA⊥BD．
又PA∩AC=A，∴BD⊥平面PAC．
∴BD⊥PC．
（2）解：分别以AB，AD，AP为x轴，y轴，z轴建立如图的空间直角坐标系，
∴B（4，0，0），C（2，2
，0），D（0，
，0），P（0，0，4）．
设平面PBC的一个法向量为
=（x，y，z），则
∵
=（2，2
，-4），
=（4，0，-4），
∴
，
令z=3，得x=3，y=
，则平面PBC的一个法向量为
=（3，
，3），
同理可求平面DPC的法向量
=（-1，
，1）．
设二面角D-PC-B的大小为θ，则cosθ=
=
．
∴二面角D-PC-B余弦值为
．
∴BM⊥AC，即BD⊥AC．
又∵PA⊥平面ABCD，∴PA⊥BD．
又PA∩AC=A，∴BD⊥平面PAC．
∴BD⊥PC．
（2）解：分别以AB，AD，AP为x轴，y轴，z轴建立如图的空间直角坐标系，
∴B（4，0，0），C（2，2
| 3 |
4
| ||
| 3 |
设平面PBC的一个法向量为
| n |
∵
| PC |
| 3 |
| PB |
∴
|
令z=3，得x=3，y=
| 3 |
| n |
| 3 |
同理可求平面DPC的法向量
| m |
| 3 |
设二面角D-PC-B的大小为θ，则cosθ=
| |-3+3+3| | ||||
|
| ||
| 35 |
∴二面角D-PC-B余弦值为
| ||
| 35 |
点评：本题考查线面垂直的判定定理与性质，考查二面角，考查学生分析解决问题的能力，考查向量法的运用，确定平面的法向量是关键．
练习册系列答案
阅读快车系列答案
相关题目