题目内容
5.函数y=log2(x+2)的定义域是( )| A. | (-∞,-2) | B. | (-∞,-2] | C. | (-2,+∞) | D. | [-2,+∞) |
分析 根据对数函数的真数大于0,列出不等式求出解集即可.
解答 解:函数y=log2(x+2),
∴x+2>0,
解得x>-2,
∴函数y的定义域是(-2,+∞).
故选:C.
点评 本题考查了求对数函数的定义域的应用问题,是基础题目.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
20.为了得到函数$y=cos(2x-\frac{π}{2})$的图象,可以将函数y=cos2x的图象( )
| A. | 向左平移$\frac{π}{2}$个单位长度 | B. | 向左平移$\frac{π}{4}$个单位长度 | ||
| C. | 向右平移$\frac{π}{2}$个单位长度 | D. | 向右平移$\frac{π}{4}$个单位长度 |
13.函数f(x)=cos2x的周期是T,将f(x)的图象向右平移$\frac{T}{4}$个单位长度后得到函数g(x),则g(x)具有性质( )
| A. | 最大值为1,图象关于直线x=$\frac{π}{2}$对称 | B. | 在(0,$\frac{π}{4}$)上单调递增,为奇函数 | ||
| C. | 在($-\frac{3π}{8}$,$\frac{π}{8}$)上单点递增,为偶函数 | D. | 周期为π,图象关于点($\frac{3π}{8}$,0)对称 |
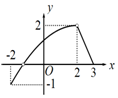


 已知函数f(x)=sin(ωx+φ)$({ω>0,|φ|<\frac{π}{2}})$一个周期的图象(如图),则这个函数的解析式为f(x)=$sin(2x+\frac{π}{6})$.
已知函数f(x)=sin(ωx+φ)$({ω>0,|φ|<\frac{π}{2}})$一个周期的图象(如图),则这个函数的解析式为f(x)=$sin(2x+\frac{π}{6})$. ,且
,且 ,则
,则 的值是 ( )
的值是 ( ) C.
C. D.400
D.400