题目内容
1.已知M是球O半径OP的中点,过M做垂直于OP的平面,截球面得圆O1,则以圆O1为大圆的球与球O的体积比是$\frac{3}{8}\sqrt{3}$.分析 由题意,设出圆M的半径,球的半径,二者与OM构成直角三角形,求出半径关系,然后可求以圆O1为大圆的球与球O的体积比.
解答 解:由题意,设出圆M的半径r,球的半径R,
由勾股定理得R2=r2+($\frac{R}{2}$)2,r=$\frac{\sqrt{3}}{2}$R.
∴以圆O1为大圆的球与球O的体积比是$\frac{3}{8}\sqrt{3}$.
故答案为:$\frac{3}{8}\sqrt{3}$.
点评 本题是基础题,考查球的体积的计算,理解并能够应用小圆的半径、球的半径、以及球心与圆心的连线的关系,是本题的突破口,解题重点所在,仔细体会.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
13.已知空间两不同直线m、n,两不同平面α、β,下列命题正确的是( )
| A. | 若m∥α且n∥α,则m∥n | B. | 若m⊥β且m⊥n,则n∥β | ||
| C. | 若m⊥α且m∥β,则α⊥β | D. | 若m不垂直于α,且n?α则m不垂直于n |
13.直线y=kx+3与圆(x-2)2+(y-3)2=4相交于M,N两点,若|MN|≥2,则k的取值范围是( )
| A. | $[-\sqrt{3},\sqrt{3}]$ | B. | $(-∞,-\sqrt{3}]∪[\sqrt{3},+∞)$ | C. | $[-\frac{{\sqrt{3}}}{3},\frac{{\sqrt{3}}}{3}]$ | D. | $[-\frac{2}{3},0]$ |
9.若复数$\frac{a+i}{1+2i}$(a∈R)为纯虚数,其中i为虚数单位,则a=( )
| A. | 2 | B. | 3 | C. | -2 | D. | -3 |
6.已知函数f(x)=sin(ωx-$\frac{π}{6}$)+$\frac{1}{2}$(ω>0),且f(a)=-$\frac{1}{2}$,f(β)=$\frac{1}{2}$,若|α-β|的最小值为$\frac{3π}{4}$,则函数的单调递增区间为( )
| A. | [-$\frac{π}{2}$+2kπ,π+2kπ],k∈Z | B. | [-$\frac{π}{2}$+3kπ,π+3kπ],k∈Z | ||
| C. | [π+2kπ,$\frac{5π}{2}$+2kπ],k∈Z | D. | [π+3kπ,$\frac{5π}{2}$+3kπ],k∈Z |
10.设函数f(x)(x∈R)满足f(x-π)=f(x)+sinx,当0≤x≤π,f(x)=1时,则$f({-\frac{13π}{6}})$=( )
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | $-\frac{3}{2}$ |
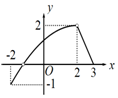


 已知函数f(x)=sin(ωx+φ)$({ω>0,|φ|<\frac{π}{2}})$一个周期的图象(如图),则这个函数的解析式为f(x)=$sin(2x+\frac{π}{6})$.
已知函数f(x)=sin(ωx+φ)$({ω>0,|φ|<\frac{π}{2}})$一个周期的图象(如图),则这个函数的解析式为f(x)=$sin(2x+\frac{π}{6})$.