题目内容
已知点Q是抛物线C1:y2=2px(p>0)上异于坐标原点O的点,过点Q与抛物线C2:y=2x2相切的两条直线分别交抛物线C1于点A,B.若点Q的坐标为(1,-6),求直线AB的方程及弦AB的长.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:先求出抛物线C1的方程,设抛物线C2的切线方程为y+6=k(x-1),与抛物线C2:y=2x2联立,由于直线与抛物线C2相切,故△=k2-8k-48=0,解得k=-4或k=12,即可求直线AB的方程及弦AB的长.
解答:
解:由Q(1,-6)在抛物线C1:y2=2px(p>0)上,可得p=18,
所以抛物线C1的方程为y2=36x.…(3分)
设抛物线C2的切线方程为y+6=k(x-1),
联立
,得2x2-kx+(k+6)=0,…(6分)
由于直线与抛物线C2相切,故△=k2-8k-48=0,解得k=-4或k=12.…(8分)
由
得A(
,-3);由
得B(
,9).…(10分)
所以直线AB的方程为12x-2y-9=0,弦AB的长为2
.…(12分)
所以抛物线C1的方程为y2=36x.…(3分)
设抛物线C2的切线方程为y+6=k(x-1),
联立
|
由于直线与抛物线C2相切,故△=k2-8k-48=0,解得k=-4或k=12.…(8分)
由
|
| 1 |
| 4 |
|
| 9 |
| 4 |
所以直线AB的方程为12x-2y-9=0,弦AB的长为2
| 37 |
点评:本题考查抛物线方程,考查直线与抛物线的位置关系,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
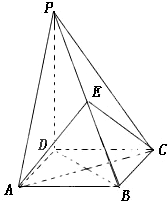 如图,四棱锥P--ABCD的底面是正方形,PD⊥底面ABCD,点E为PB的中点.且PD=
如图,四棱锥P--ABCD的底面是正方形,PD⊥底面ABCD,点E为PB的中点.且PD= 如图,正三棱柱ABC-A1B1C1的侧棱长和底面边长均为2,D是BC的中点.
如图,正三棱柱ABC-A1B1C1的侧棱长和底面边长均为2,D是BC的中点.