题目内容
已知函数f(x)=x2-2ax+4b2,a,b∈R.
(Ⅰ)若a从集合{3,4,5}中任取一个元素,b从集合{1,2,3}中任取一个元素,求方程f(x)=0有两个不相等实根的概率;
(Ⅱ)若a从区间[0,2]中任取一个数,b从区间[0,3]中任取一个数,求方程f(x)=0没有实根的概率.
(Ⅰ)若a从集合{3,4,5}中任取一个元素,b从集合{1,2,3}中任取一个元素,求方程f(x)=0有两个不相等实根的概率;
(Ⅱ)若a从区间[0,2]中任取一个数,b从区间[0,3]中任取一个数,求方程f(x)=0没有实根的概率.
考点:几何概型
专题:概率与统计
分析:分析:(Ⅰ)因为a,b∈Z,且a∈A,b∈B,这是一个古典概型,设事件E为““方程f(x)=0有两个不相等的实根”为事件A,分别算出基本事件个数和事件A中包含的基本事件,最后根据概率公式即可求得事件E的概率.
(2)由已知化简集合A和B,设事件“x∈A∩B”的概率为P1,这是一个几何概型,测度是长度,代入几何概型的计算公式即可;
(2)由已知化简集合A和B,设事件“x∈A∩B”的概率为P1,这是一个几何概型,测度是长度,代入几何概型的计算公式即可;
解答:
解:设“方程f(x)=0有两个不相等的实根”为事件A,
当a>0,b>0时,方程f(x)=0有两个不相等实根的充要条件为a>2b.
当a>2b时,a,b取值的情况有(3,1),(4,1),(5,1),(5,2),
即A包含的基本事件数为4,而基本事件总数为9.
∴方程f(x)=0有两个不相等实根的概率P(A)=
;
(2)由已知a∈A=x|0<x<2},b∈B=x|0<x<3},(2分)
设事件“方程f(x)=0没有实根”为事件B,
当a>0,b>0时,方程f(x)=0没有实根的充要条件为a<2b,
这是一个几何概型,则P(B)=
=
当a>0,b>0时,方程f(x)=0有两个不相等实根的充要条件为a>2b.
当a>2b时,a,b取值的情况有(3,1),(4,1),(5,1),(5,2),
即A包含的基本事件数为4,而基本事件总数为9.
∴方程f(x)=0有两个不相等实根的概率P(A)=
| 4 |
| 9 |
(2)由已知a∈A=x|0<x<2},b∈B=x|0<x<3},(2分)
设事件“方程f(x)=0没有实根”为事件B,
当a>0,b>0时,方程f(x)=0没有实根的充要条件为a<2b,
这是一个几何概型,则P(B)=
| ||
| 2×3 |
| 3 |
| 8 |
点评:本小题主要考查古典概型、几何概型等基础知识.古典概型与几何概型的主要区别在于:几何概型是另一类等可能概型,它与古典概型的区别在于试验的结果不是有限个,简单地说,如果每个事件发生的概率只与构成该事件区域的长度(面积或体积)成比例,则称这样的概率模型为几何概率模型,简称为几何概型.

练习册系列答案
 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
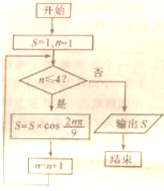
阅读如图所示的程序框图,则输出结果S的值为( )

A、-
| ||
B、-
| ||
C、
| ||
D、
|
已知F1、F2分别为椭圆C的两个焦点,点B为其短轴的一个端点,若△BF1F2为等边三角形,则该椭圆的离心率为( )
| A、2 | ||||
B、
| ||||
C、
| ||||
D、
|
函数y=x2lg
的图象( )
| x-2 |
| x+2 |
| A、关于x轴对称 |
| B、关于原点对称 |
| C、关于直线y=x对称 |
| D、关于y轴对称 |
在△ABC中,a,b,c分别为角A、B、C的对边,已知∠A=60°,b=1,面积S=
,则
等于( )
| 3 |
| a+b+c |
| sinA+sinB+sinC |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知四棱锥底面是边长为2的正方形,侧棱长均为2,则侧面与底面所成二面角的余弦值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|