Question

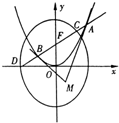已知过抛物线x²=4y的焦点F的直线l与抛物线相交于A、B两点．
（1）设抛物线在A、B处的切线的交点为M，若点M的横坐标为2，求△ABM的外接圆方程．
（2）若直线l与椭圆

3y2

4

+

3x2

2

=1的交点为C，D，问是否存在这样的直线l使|AF|•|CF|=|BF|•|DF|，若存在，求出l的方程；若不存在，说明理由．

Answer 1

考点：直线与圆锥曲线的综合问题

专题：圆锥曲线中的最值与范围问题

分析：（1）设A(2t1，

t

2 1

)，B(2t2，

t

2 2

)，kAB=

t 2 1 - t 2 2

2t1-2t2

=

t1+t2

2

，直线AB：y-

t

2 1

=

t1+t2

2

(x-2t1)，从而得到过A，B，M的圆是以AB为直径的圆，由此结合已知条件能求出圆的方程．
（2）设

|AF|

|BF|

=

|DF|

|CF|

=λ，则

AF

=λ

FB

，

DF

=λ

FC

，由此利用韦达定理，结合已知条件能求出满足条件的直线方程．

解答： 解：（1）设A(2t1，

t

2 1

)，B(2t2，

t

2 2

)，kAB=

t 2 1 - t 2 2

2t1-2t2

=

t1+t2

2

故AB：y-

t

2 1

=

t1+t2

2

(x-2t1)
过（0，1）得-t1t2=1，又由y=

1

4

x2，得y′=

1

2

x
故kMA•kMB=

1

2

×(2t1)×

1

2

×(2t2)=t1t2=-1
∴过A，B，M的圆是以AB为直径的圆
又MA：y-

t

2 1

=t1(x-2t1)，MB：y-

t

2 2

=t2(x-2t2)
即

t

2 1

-t1x+y=0，且

t

2 2

-t2x+y=0
联立两式解得x_M=t₁+t₂=2，y_M=t₁t₂=-1
故AB的中点G坐标为（2，3），|GM|=4
所求圆的方程为（x-2）²+（y-3）²=16．…（6分）
（2）设

|AF|

|BF|

=

|DF|

|CF|

=λ，则

AF

=λ

FB

，

DF

=λ

FC

设A（x₁，y₁），B（x₂，y₂），C（x₃，y₃），D（x₄，y₄），
则

-x1=λx2 -x4=λx3

⇒

x1=-λx2 x4=-λx3

又

y=kx+1 x2=4y

⇒x2-4kx-4=0，
∴x₁+x₂=4k，x₁x₂=-4
将x1=-λx2，代入得

(λ-1)2

λ

=4k2，…①
由

y=kx+1 3y2 4 + 3x2 2 =1

=(3k2+6)x2+6kx-1=0∴x3+x4=-

2k

k2+2

，x3x4=-

1

3k2+6

将x4=-λx3，代入得

(λ-1)2

λ

=

12k2

k2+2

，
由①②得k=0或k²=1，k=±1，
经检验k=±1时，A、B、C、D四点各异，且满足要求
故直线l存在，且方程为y=±x+1．…（13分）

点评：本题考查三角形外接圆方程的求法，考查满足条件的直线方程是否存在的判断与求法，解题时要注意函数与方程思想的合理运用，