题目内容
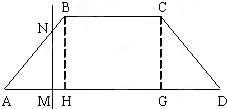 如图,等腰梯形ABCD的两底分别为AD=2a,BC=a,∠BAD=45°,作直线NM⊥AD交AD于M,交折线ABCD于N,设AM=x,试将梯形ABCD位于直线MN左侧的面积y表示为关于x的函数,并写出算法的伪代码及画出流程图.
如图,等腰梯形ABCD的两底分别为AD=2a,BC=a,∠BAD=45°,作直线NM⊥AD交AD于M,交折线ABCD于N,设AM=x,试将梯形ABCD位于直线MN左侧的面积y表示为关于x的函数,并写出算法的伪代码及画出流程图.考点:设计程序框图解决实际问题
专题:综合题,函数的性质及应用,算法和程序框图
分析:直线MN左侧的面积的计算方法与MN所处的位置不同计算方式不同,MN所处的位置可分为三种情况:M在A,H之间,M在H,G之间或M在G,D之间,所以分三段计算求解.
解答:
解:作BH⊥AD,H为垂足,CG⊥AD,G为垂足,
依题意,则有AH=
,AG=
a.
(1)当M位于点H的左侧时,N∈AB,由于AM=x,∠BAD=45°,∴MN=x.
∴y=S△AMN=
x2(0≤x≤
).
(2)当M位于HG之间时,
由于AM=x,∠BAD=45°,∴MN=
,BN=x-
.
∴y=S直角梯形AMNB=
•
[x+(x-
)]=
ax-
(
<x≤
a).
(3)当M位于点G的右侧时,
由于AM=x,MN=MD=2a-x,
∴y=S梯形ABCD-S△MDN=
•
(2a+a)-
(2a-x)2=-
x2+2ax-
(
a<x≤2a).
Read x
If 0<x≤
then
y←
x2
Else if
<x≤
a then
y←
ax-
Else
y←-
x2+2ax-
End if
Print y
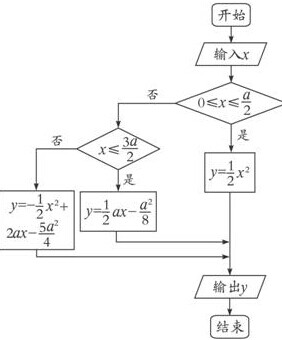
程序框图如下:
依题意,则有AH=
| a |
| 2 |
| 3 |
| 2 |
(1)当M位于点H的左侧时,N∈AB,由于AM=x,∠BAD=45°,∴MN=x.
∴y=S△AMN=
| 1 |
| 2 |
| a |
| 2 |
(2)当M位于HG之间时,
由于AM=x,∠BAD=45°,∴MN=
| a |
| 2 |
| a |
| 2 |
∴y=S直角梯形AMNB=
| 1 |
| 2 |
| a |
| 2 |
| a |
| 2 |
| 1 |
| 2 |
| a2 |
| 8 |
| a |
| 2 |
| 3 |
| 2 |
(3)当M位于点G的右侧时,
由于AM=x,MN=MD=2a-x,
∴y=S梯形ABCD-S△MDN=
| 1 |
| 2 |
| a |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5a2 |
| 4 |
| 3 |
| 2 |
Read x
If 0<x≤
| a |
| 2 |
y←
| 1 |
| 8 |
Else if
| a |
| 2 |
| 3 |
| 2 |
y←
| 1 |
| 2 |
| a2 |
| 8 |
Else
y←-
| 1 |
| 2 |
| 5a2 |
| 4 |
End if
Print y
程序框图如下:

点评:本题属于一道分段函数的应用问题,属于一个中档题,能有效考查学生综合运用知识解决问题的能力.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目