题目内容
在△ABC中,角A,B,C的对边分别为a,b,c,且满足asinC=
ccosA,
•
=2.
(Ⅰ)求角A;
(Ⅱ)求△ABC的面积;
(Ⅲ)若b=1,求边c与a的值.
| 3 |
| AB |
| AC |
(Ⅰ)求角A;
(Ⅱ)求△ABC的面积;
(Ⅲ)若b=1,求边c与a的值.
考点:正弦定理,平面向量数量积的运算,余弦定理
专题:解三角形
分析:(Ⅰ)利用正弦定理把边转化成角的正弦,化简求得tanA的值,则A可得.
(Ⅱ)根据数量积公式求得bc的值,进而利用三角形面积公式求得三角形的面积.
(Ⅲ)根据第二问bc的关系求得c,最后利用余弦定理求得a.
(Ⅱ)根据数量积公式求得bc的值,进而利用三角形面积公式求得三角形的面积.
(Ⅲ)根据第二问bc的关系求得c,最后利用余弦定理求得a.
解答:
解:(Ⅰ)∵asinC=
cosA,
∴sinAsinC=
sinCcosA,
∴snA=
cosA,tanA=
,
∴A=60°
(Ⅱ)∵
•
=2,
∴b•c•cosA=2,
bc=4,
∴S=
bcsinA=
×4×
=
.
(Ⅲ)∵b=1,bc=4,
∴c=4,
由余弦定理得a=
=
.
| 3 |
∴sinAsinC=
| 3 |
∴snA=
| 3 |
| 3 |
∴A=60°
(Ⅱ)∵
| AB |
| AC |
∴b•c•cosA=2,
bc=4,
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
(Ⅲ)∵b=1,bc=4,
∴c=4,
由余弦定理得a=
| b2+c2-2bccosA |
| 13 |
点评:本题主要考查了正弦定理的应用,向量的数量积的运算.考查了学生的基础知识的灵活运用,和基础的运算能力.

练习册系列答案
相关题目
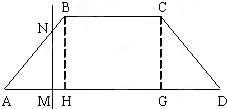 如图,等腰梯形ABCD的两底分别为AD=2a,BC=a,∠BAD=45°,作直线NM⊥AD交AD于M,交折线ABCD于N,设AM=x,试将梯形ABCD位于直线MN左侧的面积y表示为关于x的函数,并写出算法的伪代码及画出流程图.
如图,等腰梯形ABCD的两底分别为AD=2a,BC=a,∠BAD=45°,作直线NM⊥AD交AD于M,交折线ABCD于N,设AM=x,试将梯形ABCD位于直线MN左侧的面积y表示为关于x的函数,并写出算法的伪代码及画出流程图.