题目内容
已知函数f(x)=|x2-ax+a|(a>0),则f(x)的单调递增区间是 .
考点:函数的单调性及单调区间
专题:函数的性质及应用
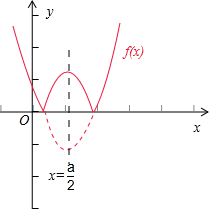
分析:画出函数f(x)=|x2-ax+a|(a>0)的图象,数形结合可得f(x)的单调递增区间.
解答:
 解:对于y=x2-ax+a,它的判别式△=a(a-4),
解:对于y=x2-ax+a,它的判别式△=a(a-4),
当0<a<4时,△<0,函数y=x2-ax+a的图象和x轴没有交点,
f(x)=x2-ax+a,此时,f(x)的增区间为[
,+∞).
当a≥4时,△≥0,由=x2-ax+a=0,求得
可得x=
,或 x=
,
故此时函数f(x)=|x2-ax+a|(a>0)的图象如图所示:
故函数的增区间为[
,
]、[
,+∞),
故答案为:当0<a<4时,[
,+∞);
当a≥4时,[
,
]、[
,+∞).
 解:对于y=x2-ax+a,它的判别式△=a(a-4),
解:对于y=x2-ax+a,它的判别式△=a(a-4),当0<a<4时,△<0,函数y=x2-ax+a的图象和x轴没有交点,
f(x)=x2-ax+a,此时,f(x)的增区间为[
| a |
| 2 |
当a≥4时,△≥0,由=x2-ax+a=0,求得
可得x=
a-
| ||
| 2 |
a+
| ||
| 2 |
故此时函数f(x)=|x2-ax+a|(a>0)的图象如图所示:
故函数的增区间为[
a-
| ||
| 2 |
| a |
| 2 |
a+
| ||
| 2 |
故答案为:当0<a<4时,[
| a |
| 2 |
当a≥4时,[
a-
| ||
| 2 |
| a |
| 2 |
a+
| ||
| 2 |
点评:本题主要考查函数的单调性和单调区间,体现了数形结合、分类讨论的数学思想,属于基础题.

练习册系列答案
相关题目
方程7x2-(k+3)x+k2-k-2=0有两个实数根x1,x2,且0<x1<1<x2<2,则实数k的取值范围是( )
| A、(-2,-1) |
| B、(3,4) |
| C、(-2,4) |
| D、(-2,-1)∪(3,4) |
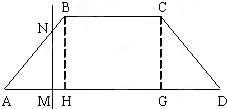 如图,等腰梯形ABCD的两底分别为AD=2a,BC=a,∠BAD=45°,作直线NM⊥AD交AD于M,交折线ABCD于N,设AM=x,试将梯形ABCD位于直线MN左侧的面积y表示为关于x的函数,并写出算法的伪代码及画出流程图.
如图,等腰梯形ABCD的两底分别为AD=2a,BC=a,∠BAD=45°,作直线NM⊥AD交AD于M,交折线ABCD于N,设AM=x,试将梯形ABCD位于直线MN左侧的面积y表示为关于x的函数,并写出算法的伪代码及画出流程图.