题目内容
已知函数f（x）=2x2+4x，求出函数f（x）的单调区间，并对减区间的情况给予证明．
考点：函数单调性的判断与证明,二次函数的性质
专题：函数的性质及应用
分析：利用导函数值的正负来找原函数的单调区间和证明其单调性
解答：
解：f（x）=2x2+4x，∴f′（x）=4x+4，
由f′（x）＞0，得：x＞-1，f′（x）＜0，得：x＜-1，
∴f（x）在（-∞，-1）递减，在（-1，+∞）递增．
由f′（x）＞0，得：x＞-1，f′（x）＜0，得：x＜-1，
∴f（x）在（-∞，-1）递减，在（-1，+∞）递增．
点评：求函数的单调区间时，一般可以应用以下方法：①定义法，②图象法，③借助其他函数的单调性判断法，④利用导函数法等
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
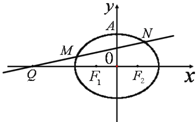如图，已知椭圆C：
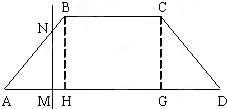如图，等腰梯形ABCD的两底分别为AD=2a，BC=a，∠BAD=45°，作直线NM⊥AD交AD于M，交折线ABCD于N，设AM=x，试将梯形ABCD位于直线MN左侧的面积y表示为关于x的函数，并写出算法的伪代码及画出流程图．