题目内容
已知F1、F2分别是椭圆的左、右焦点,A是椭圆
+y2=1上一动点,圆C与F1A的延长线,F1F2的延长线以及线段AF2相切,若M(t,0)为其中一个切点,则( )
| x2 |
| 4 |
| A、t=2 |
| B、t>2 |
| C、t<2 |
| D、t与2的大小关系不确定 |
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:如图所示,切点分别为M,N,E.利用切线的性质可得|F1F2|+|F2M|=|F1A|+|AE|,|AE|=|AN|,|F2M|=|F2N|.利用椭圆的定义可得|F1A|+|AN|+|NF2|=2a=4,即可解出.
解答:
解:如图所示,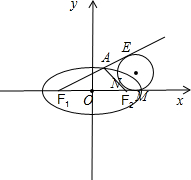 切点分别为M,N,E.
切点分别为M,N,E.
∵|F1F2|+|F2M|=|F1A|+|AE|,|AE|=|AN|,|F2M|=|F2N|.
|F1A|+|AN|+|NF2|=2a=4,
∴
+t=4-(t-
),
解得t=2.
故选:A.
 切点分别为M,N,E.
切点分别为M,N,E.∵|F1F2|+|F2M|=|F1A|+|AE|,|AE|=|AN|,|F2M|=|F2N|.
|F1A|+|AN|+|NF2|=2a=4,
∴
| 3 |
| 3 |
解得t=2.
故选:A.
点评:本题考查了圆的切线的性质、椭圆的定义,考查了推理能力与计算能力,属于难题.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
下列推理正确的是( )
| A、把a(b+c)与loga(x+y)类比,则有loga(x+y)=logax+logay |
| B、把a(b+c)与sin(x+y)类比,则有sin(x+y)=sinx+siny |
| C、把a(b+c)与ax+y类比,则有ax+y=ax+ay |
| D、把a(b+c)与a*(b+c)类比,则有a*(b+c)=a*b+a* |
已知x,y的取值如表所示,若y与x线性相关,且
=0.95x+a,则a=( )
 |
| y |
| x | 0 | 1 | 3 | 4 |
| y | 2.2 | 4.3 | 4.8 | 6.7 |
| A、2.2 | B、2.6 |
| C、2.8 | D、2.9 |
在几何体P-ABCD中,ABCD为矩形,各棱所在直线共有异面直线( )


| A、4对 |
| B、6对 |
| C、8对 |
| D、12对 ( |
 如图,边长为2的正方体ABCD-A1B1C1D1中,E、F分别是棱A1D1,B1C1的中点.
如图,边长为2的正方体ABCD-A1B1C1D1中,E、F分别是棱A1D1,B1C1的中点. 已知函数f(x)是定义在[-5,5]上的偶函数,且当x≤0时,f(x)=x2+4x
已知函数f(x)是定义在[-5,5]上的偶函数,且当x≤0时,f(x)=x2+4x