题目内容
已知函数f(x)=
,令an=f(
) (k∈N*,n=1,2,3,…,k),则数列{an}的前k项和Sk= .
| 1 |
| 2+4x |
| n |
| k |
考点:数列的求和
专题:点列、递归数列与数学归纳法
分析:由已知函数得到f(x)+f(1-x)=
,再求出f(1)的值,然后利用倒序相加法求得数列{an}的前k项和Sk
| 1 |
| 2 |
解答:
解:∵f(x)=
,
则f(x)+f(1-x)=
+
=
+
=
+
=
=
=
,
∴Sk=a1+a2+a3+…+ak
=f(
)+f(
)+…+f(
)+f(1)①,
Sk=f(
)+f(
)+…+f(
)+f(1) ②,
两式相加得:2Sk=
+2f(1),
Sk=
+f(1),
由f(x)=
,得f(1)=
,
∴Sk=
+
=
.
故答案为:
.
| 1 |
| 2+4x |
则f(x)+f(1-x)=
| 1 |
| 2+4x |
| 1 |
| 2+41-x |
=
| 1 |
| 2+4x |
| 1 | ||
2+
|
| 1 |
| 2+4x |
| 4x |
| 2•4x+4 |
=
| 2•4x+4+2•4x+(4x)2 |
| (2+4x)(2•4x+4) |
| (4x)2+4•4x+4 |
| 2[(4x)2+4•4x+4] |
| 1 |
| 2 |
∴Sk=a1+a2+a3+…+ak
=f(
| 1 |
| k |
| 2 |
| k |
| k-1 |
| k |
Sk=f(
| k-1 |
| k |
| k-2 |
| k |
| 1 |
| k |
两式相加得:2Sk=
| k-1 |
| 2 |
Sk=
| k-1 |
| 4 |
由f(x)=
| 1 |
| 2+4x |
| 1 |
| 6 |
∴Sk=
| k-1 |
| 4 |
| 1 |
| 6 |
| 3k-1 |
| 12 |
故答案为:
| 3k-1 |
| 12 |
点评:本题考查了数列的函数特性,关键是在理解题意的基础上求得f(x)+f(1-x)=
,训练了倒序相加法求数列的和,是中档题.
| 1 |
| 2 |

练习册系列答案
相关题目
在△ABC中,角A,B,C所对的边分别为a,b,c,A:B:C=3:1:2,则a:b:c=( )
| A、1:2:3 | ||
| B、3:1:2 | ||
C、1:
| ||
D、2:1:
|
在如图的程序框图中,该程序框图输出的结果是28,则序号①应填入的条件是( ) 

| A、K≤4? | B、K≥4? |
| C、K<4? | D、K>4? |
如果椭圆4x2+y2=k上两点间的最大距离是8,那么k等于( )
| A、32 | B、16 | C、8 | D、4 |
已知F1、F2分别是椭圆的左、右焦点,A是椭圆
+y2=1上一动点,圆C与F1A的延长线,F1F2的延长线以及线段AF2相切,若M(t,0)为其中一个切点,则( )
| x2 |
| 4 |
| A、t=2 |
| B、t>2 |
| C、t<2 |
| D、t与2的大小关系不确定 |
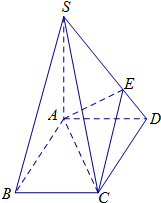 如图,在四棱锥S-ABCD中,底面ABCD为平行四边形,SA⊥底面ABCD,SA=AB=2,AD=1,∠ABC=60°,E在棱SD上.
如图,在四棱锥S-ABCD中,底面ABCD为平行四边形,SA⊥底面ABCD,SA=AB=2,AD=1,∠ABC=60°,E在棱SD上.