题目内容
一段长为16m的篱笆围成一个一边靠墙的矩形菜园,则这个矩形的长为 m时菜园的面积最大,最大的面积是 m2.
考点:函数的最值及其几何意义
专题:应用题,函数的性质及应用
分析:由题意设矩形的长为xm,宽为
m,从而表示出S=x•
,利用基本不等式求解.
| 16-x |
| 2 |
| 16-x |
| 2 |
解答:
解:设矩形的长为xm,宽为
m,
则S=x•
≤
(
)2=32.
(当且仅当x=16-x,即x=8时,等号成立)
故答案为:8,32.
| 16-x |
| 2 |
则S=x•
| 16-x |
| 2 |
| 1 |
| 2 |
| x+16-x |
| 2 |
(当且仅当x=16-x,即x=8时,等号成立)
故答案为:8,32.
点评:本题考查了实际问题转化为数学问题的能力及基本不等式的应用,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知F1、F2分别是椭圆的左、右焦点,A是椭圆
+y2=1上一动点,圆C与F1A的延长线,F1F2的延长线以及线段AF2相切,若M(t,0)为其中一个切点,则( )
| x2 |
| 4 |
| A、t=2 |
| B、t>2 |
| C、t<2 |
| D、t与2的大小关系不确定 |
从装有2个红球和2个黒球的口袋内任取2个球,则互斥而不对立的两个事件是( )
| A、“至少有一个黑球”与“都是红球” |
| B、“至少有一个黒球”与“都是黒球” |
| C、“恰有m个黒球”与“恰有2个黒球” |
| D、“至少有一个黒球”与“至少有1个红球” |
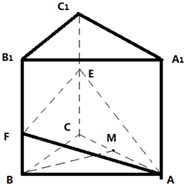 如图,直三棱柱ABC-A1B1C1中,底面是边长为2的正三角形,点E,F分别是
如图,直三棱柱ABC-A1B1C1中,底面是边长为2的正三角形,点E,F分别是