题目内容
 如图,边长为2的正方体ABCD-A1B1C1D1中,E、F分别是棱A1D1,B1C1的中点.
如图,边长为2的正方体ABCD-A1B1C1D1中,E、F分别是棱A1D1,B1C1的中点.(Ⅰ)求异面直线AE与FC所成角的余弦值;
(Ⅱ)求直线AC1与平面B1BCC1所成角的正切值.
考点:直线与平面所成的角,异面直线及其所成的角
专题:空间角
分析:(1)因为E、F分别是棱A1D1,B1C1的中点,连接BF,则BF∥AE,所以∠BFC为异面直线AE与FC所成角,利用余弦定理求余弦值;
(2)因为AB⊥平面B1BCC1,所以∠AC1B为直线AC1与平面B1BCC1所成角.
(2)因为AB⊥平面B1BCC1,所以∠AC1B为直线AC1与平面B1BCC1所成角.
解答:
解:(1)在正方体ABCD-A1B1C1D1中,E、F分别是棱A1D1,B1C1的中点.连接BF,则EF∥AB,所以BF∥AE,所以∠BFC为异面直线AE与FC所成角,
cos∠BFC=
=
=
,
所以异面直线AE与FC所成角的余弦值为
.
(2)因为AB⊥平面B1BCC1,所以∠AC1B为直线AC1与平面B1BCC1所成角,tan∠AC1B=
=
=
;
直线AC1与平面B1BCC1所成角的正切值
.
cos∠BFC=
| BF2+CF2-BC2 |
| 2BF×CF |
| 5+5-4 | ||||
2
|
| 3 |
| 5 |
所以异面直线AE与FC所成角的余弦值为
| 3 |
| 5 |
(2)因为AB⊥平面B1BCC1,所以∠AC1B为直线AC1与平面B1BCC1所成角,tan∠AC1B=
| AB |
| BC1 |
| 2 | ||
2
|
| ||
| 2 |
直线AC1与平面B1BCC1所成角的正切值
| ||
| 2 |
点评:本题考查异面直线所成的角以及线面角的求法,考查学生分析解决问题、转化的能力,属于中档题.

练习册系列答案
相关题目
如果椭圆4x2+y2=k上两点间的最大距离是8,那么k等于( )
| A、32 | B、16 | C、8 | D、4 |
以边长为1的正方形的一条边为旋转轴,旋转一周后所得旋转体侧面积为( )
| A、2π | B、π | C、2 | D、1 |
设F1,F2分别为双曲线
-
=1(a>0,b>0)的左、右焦点,若在右支上存在点A,使得点F2到直线AF1的距离为2a,则该双曲线的离心率的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、(1,
| ||
B、(
| ||
| C、(1,2) | ||
| D、(2,+∞) |
已知F1、F2分别是椭圆的左、右焦点,A是椭圆
+y2=1上一动点,圆C与F1A的延长线,F1F2的延长线以及线段AF2相切,若M(t,0)为其中一个切点,则( )
| x2 |
| 4 |
| A、t=2 |
| B、t>2 |
| C、t<2 |
| D、t与2的大小关系不确定 |
下列函数在(-∞,0)上为增函数的是( )
| A、y=x3 | ||
| B、y=x2 | ||
| C、y=|x| | ||
D、y=(
|
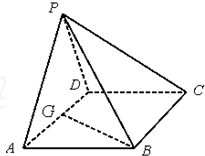 如图,在四棱锥P-ABCD中,底面ABCD是∠DAB=60°且边长为a的菱形,侧面PAD是等边三角形,且平面PAD⊥底面ABCD,G为AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是∠DAB=60°且边长为a的菱形,侧面PAD是等边三角形,且平面PAD⊥底面ABCD,G为AD的中点.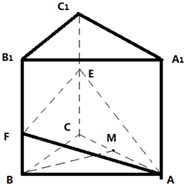 如图,直三棱柱ABC-A1B1C1中,底面是边长为2的正三角形,点E,F分别是
如图,直三棱柱ABC-A1B1C1中,底面是边长为2的正三角形,点E,F分别是