题目内容
 已知函数f(x)是定义在[-5,5]上的偶函数,且当x≤0时,f(x)=x2+4x
已知函数f(x)是定义在[-5,5]上的偶函数,且当x≤0时,f(x)=x2+4x(1)画出函数f(x)的大致图象,并写出函数的单调增区间与单调减区间.
(2)若方程f(x)+2a=0有四个根,求实数a的取值范围.
考点:函数的零点与方程根的关系,函数图象的作法
专题:函数的性质及应用
分析:(1)根据偶函数的对称性即可画出函数f(x)的大致图象,并写出函数的单调增区间与单调减区间.
(2)利用数形结合即可求实数a的取值范围.
(2)利用数形结合即可求实数a的取值范围.
解答:
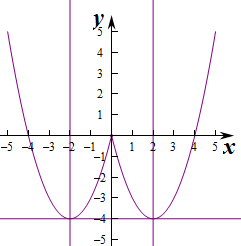 解:(1)若0≤x≤5,则-5≤-x≤0,
解:(1)若0≤x≤5,则-5≤-x≤0,
∵f(x)是定义在[-5,5]上的偶函数,且当x≤0时,f(x)=x2+4x
∴f(-x)=x2-4x=f(x),
即f(x)=x2-4x,0≤x≤5,
作出函数的图象如图:
单调增区间:(-2,0),(2,5);
单调减区间:(-5,-2),(0,2);
(2)由f(x)+2a=0得f(x)=-2a,
若方程f(x)+2a=0有四个根,
则等价为函数f(x)与y=-2a有四个不同的交点,
由图象可知-4<-2a<0,
即0<a<2,
故实数a的取值范围是(0,2).
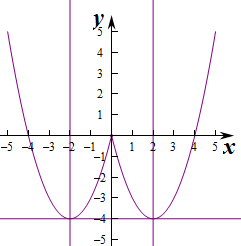 解:(1)若0≤x≤5,则-5≤-x≤0,
解:(1)若0≤x≤5,则-5≤-x≤0,∵f(x)是定义在[-5,5]上的偶函数,且当x≤0时,f(x)=x2+4x
∴f(-x)=x2-4x=f(x),
即f(x)=x2-4x,0≤x≤5,
作出函数的图象如图:
单调增区间:(-2,0),(2,5);
单调减区间:(-5,-2),(0,2);
(2)由f(x)+2a=0得f(x)=-2a,
若方程f(x)+2a=0有四个根,
则等价为函数f(x)与y=-2a有四个不同的交点,
由图象可知-4<-2a<0,
即0<a<2,
故实数a的取值范围是(0,2).
点评:本题主要考查函数的奇偶性的应用以及方程和函数的应用,利用数形结合是解决本题的关键.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
已知F1、F2分别是椭圆的左、右焦点,A是椭圆
+y2=1上一动点,圆C与F1A的延长线,F1F2的延长线以及线段AF2相切,若M(t,0)为其中一个切点,则( )
| x2 |
| 4 |
| A、t=2 |
| B、t>2 |
| C、t<2 |
| D、t与2的大小关系不确定 |
从装有2个红球和2个黒球的口袋内任取2个球,则互斥而不对立的两个事件是( )
| A、“至少有一个黑球”与“都是红球” |
| B、“至少有一个黒球”与“都是黒球” |
| C、“恰有m个黒球”与“恰有2个黒球” |
| D、“至少有一个黒球”与“至少有1个红球” |
下列函数在(-∞,0)上为增函数的是( )
| A、y=x3 | ||
| B、y=x2 | ||
| C、y=|x| | ||
D、y=(
|
已知f(x)=
,若f(x)为奇函数,则g(-1)的值为( )
|
| A、3 | B、-1 | C、-3 | D、1 |
已知点P是△ABC所在平面内一点,且满足3
+5
+2
=
,设△ABC的面积为S,则△PAB的面积为( )
| PA |
| PB |
| PC |
| 0 |
A、
| ||
B、
| ||
C、
| ||
D、
|