题目内容
已知f(x)=|x-3|-1
(1)若f(x)≥2,求x的取值范围;
(2)?x∈R,f(x)>|x+1|-|a|恒成立,求a的范围.
(1)若f(x)≥2,求x的取值范围;
(2)?x∈R,f(x)>|x+1|-|a|恒成立,求a的范围.
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:(1)由f(x)≥2,可得|x-3|≥3,由此解绝对值不等式,求得要求的x的范围.
(2)由题意可得|x-3|-|x+1|≥1-|a|恒成立,故-4≥1-|a|,即|a|≥5,由此求得a的范围.
(2)由题意可得|x-3|-|x+1|≥1-|a|恒成立,故-4≥1-|a|,即|a|≥5,由此求得a的范围.
解答:
解:(1)由f(x)≥2,可得|x-3|≥3,∴x-3≥3,或 x-3≤-3,
求得x≥6,或x≤0,故要求的x的范围为{x|x≥6,或 x≤0 }.
(2)∵?x∈R,f(x)>|x+1|-|a|恒成立,可得|x-3|-|x+1|≥1-|a|.
由于表示数轴上的x对应点到3的距离减去它到-1的距离,故|x-3|-|x+1|的最小值为-4,
由题意可得,-4≥1-|a|,即|a|≥5,求得a≥5,或a≤-5.
求得x≥6,或x≤0,故要求的x的范围为{x|x≥6,或 x≤0 }.
(2)∵?x∈R,f(x)>|x+1|-|a|恒成立,可得|x-3|-|x+1|≥1-|a|.
由于表示数轴上的x对应点到3的距离减去它到-1的距离,故|x-3|-|x+1|的最小值为-4,
由题意可得,-4≥1-|a|,即|a|≥5,求得a≥5,或a≤-5.
点评:本题主要考查绝对值不等式的解法,函数的恒成立问题,绝对值的意义,属于基础题.

练习册系列答案
相关题目
函数g(x)=4×3x的图象可看成将函数f(x)=3x的图象( )
| A、向左平移log34个单位得到 | ||
| B、各点横坐标不变,纵坐标伸长的原来的4倍得到 | ||
| C、向右平移log34个单位得到 | ||
D、各点纵坐标不变,横坐标缩短的原来的
|
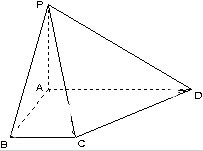 如图所示,已知ABCD是直角梯形,∠DAB=∠ABC=90°,AB=BC=a,AD=2a,P是平面ABCD外的一点,PA⊥平面ABCD,且PA=a,求点A到平面PCD的距离.
如图所示,已知ABCD是直角梯形,∠DAB=∠ABC=90°,AB=BC=a,AD=2a,P是平面ABCD外的一点,PA⊥平面ABCD,且PA=a,求点A到平面PCD的距离.