题目内容
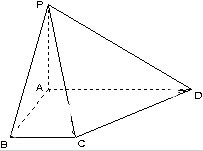 如图所示,已知ABCD是直角梯形,∠DAB=∠ABC=90°,AB=BC=a,AD=2a,P是平面ABCD外的一点,PA⊥平面ABCD,且PA=a,求点A到平面PCD的距离.
如图所示,已知ABCD是直角梯形,∠DAB=∠ABC=90°,AB=BC=a,AD=2a,P是平面ABCD外的一点,PA⊥平面ABCD,且PA=a,求点A到平面PCD的距离.考点:点、线、面间的距离计算
专题:空间位置关系与距离
分析:首先利用已知条件求出相关的线段长进一步求出S△PCD=
•
a•
a=
a2,进一步利用体积相等,VA-PCD=VP-ACD,求出结果.
| 1 |
| 2 |
| 2 |
| 3 |
| ||
| 2 |
解答:
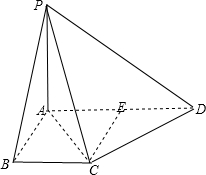 解:已知ABCD是直角梯形,取AD的中点E,
解:已知ABCD是直角梯形,取AD的中点E,
∠DAB=∠ABC=90°,AB=BC=a,AD=2a,
所以:CE=a,
PA⊥平面ABCD,且PA=a,
所以:利用勾股定理解得:CD=
a,PD=
a,PC=
a,
所以:CD2+PC2=PD2,△PCD是直角三角形.
S△PCD=
•
a•
a=
a2,
所以:VA-PCD=VP-ACD,设点A到平面PCD的距离为h,
则:
•S△PCD•h=
•S△ACD•PA,
解得:h=
a
 解:已知ABCD是直角梯形,取AD的中点E,
解:已知ABCD是直角梯形,取AD的中点E,∠DAB=∠ABC=90°,AB=BC=a,AD=2a,
所以:CE=a,
PA⊥平面ABCD,且PA=a,
所以:利用勾股定理解得:CD=
| 2 |
| 5 |
| 3 |
所以:CD2+PC2=PD2,△PCD是直角三角形.
S△PCD=
| 1 |
| 2 |
| 2 |
| 3 |
| ||
| 2 |
所以:VA-PCD=VP-ACD,设点A到平面PCD的距离为h,
则:
| 1 |
| 3 |
| 1 |
| 3 |
解得:h=
| ||
| 3 |
点评:本题考查的知识要点:勾股定理及逆定理的应用,锥体的体积运算.属于基础题型.

练习册系列答案
相关题目
二次函数f(x)=x2-2x则有( )
| A、f(3)<f(2)<f(4) |
| B、f(2)<f(3)<f(4) |
| C、f(2)<f(4)<f(3) |
| D、f(4)<f(2)<f(3) |