题目内容
 如图,设A是单位圆和x轴正半轴的交点,P,Q是单位圆上两点,O是坐标原点,且P(
如图,设A是单位圆和x轴正半轴的交点,P,Q是单位圆上两点,O是坐标原点,且P(
| ||
| 2 |
| 1 |
| 2 |
(1)若点Q的坐标是(
| 3 |
| 5 |
| 4 |
| 5 |
| π |
| 6 |
(2)设函数f(α)=
. |
| OP |
. |
| OQ |
考点:平面向量的综合题,任意角的三角函数的定义
专题:三角函数的求值,平面向量及应用
分析:第(1)问先根据三角函数的定义求出α的正余弦值,再代入两角差的余弦公式求出cos(α-
);
第(2)问先利用α的三角函数把
、
的坐标表示出来,再利用数量积的定义求出f(α),按照三角函数求知欲的方法求解,不要忽视了α的取值范围.
| π |
| 6 |
第(2)问先利用α的三角函数把
| OP |
| OQ |
解答:
解:(1)由已知可得cosα=
,sinα=
,
∴cos(α-
)=cosαcos
+sinαsin
=
×
+
×
=
.
(2)由已知得
=(
,
),
=(cosα,sinα),
∴f(α)=
•
=(
,
)•(cosα,sinα)
=
cosα+
sinα=sin
cosα+cos
sinα=sin(α+
)
∵α∈[0,π),∴α+
∈[
,
),
∴-
<sin(α+
)≤1.
故f(α)的值域是(-
,1].
| 3 |
| 5 |
| 4 |
| 5 |
∴cos(α-
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| 3 |
| 5 |
| ||
| 2 |
| 4 |
| 5 |
| 1 |
| 2 |
3
| ||
| 10 |
(2)由已知得
| OP |
| ||
| 2 |
| 1 |
| 2 |
| OQ |
∴f(α)=
| OP |
| OQ |
| ||
| 2 |
| 1 |
| 2 |
=
| ||
| 2 |
| 1 |
| 2 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
∵α∈[0,π),∴α+
| π |
| 3 |
| π |
| 3 |
| 4π |
| 3 |
∴-
| ||
| 2 |
| π |
| 3 |
故f(α)的值域是(-
| ||
| 2 |
点评:本题是一个三角函数与平面向量的综合,此类问题,要求必须对三角函数的定义及其公式,向量的基本概念和运算熟练掌握,考查的落脚点往往是三角函数的图象或性质,因此三角函数最后一般化简成形如y=Asin(ωx+θ)+C的形式.

练习册系列答案
相关题目
已知sin(π+α)=
,则cos(
-α)=( )
| 1 |
| 3 |
| 3π |
| 2 |
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
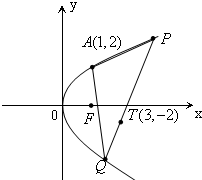 点A(1,2)到抛物线y2=2px(p>0)的焦点F的距离为2,过T(3,-2)的动直线l与此抛物线交于P、Q两点
点A(1,2)到抛物线y2=2px(p>0)的焦点F的距离为2,过T(3,-2)的动直线l与此抛物线交于P、Q两点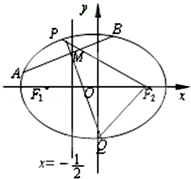 如图,F1,F2是离心率为
如图,F1,F2是离心率为