题目内容
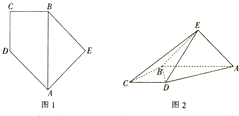 已知直角梯形ABCD的下底与等腰直角三角形ABE的斜边重合,AB⊥BC,且AB=2CD=2BC(如图1),将此图形沿AB折叠成直二面角,连接EC、ED,得到四棱锥E-ABCD(如图2).
已知直角梯形ABCD的下底与等腰直角三角形ABE的斜边重合,AB⊥BC,且AB=2CD=2BC(如图1),将此图形沿AB折叠成直二面角,连接EC、ED,得到四棱锥E-ABCD(如图2).(1)求证:在四棱锥E-ABCD中,AB⊥DE.
(2)设BC=1,求点C到平面EBD的距离.
考点:点、线、面间的距离计算,棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:(1)作AB的中点F,连结EF,DF,根据AB=2CD推断出BE=CD=BC又BE∥CD,推断出四边形BCDE为正方形,推断出DF⊥AB,根据BE=AE,F为AB的中点,推断出EF⊥AB,进而利用线面垂直的判定定理推断出AB⊥平面DEF,进而可知AB⊥DE.
(2)根据BC,分别求得AB,BE,DB,EF,DF,判断出△BDE为等边三角形,边长为
,求得其面积,最后根据SE-BCD=SC-BDE,求得点C到平面EBD的距离.
(2)根据BC,分别求得AB,BE,DB,EF,DF,判断出△BDE为等边三角形,边长为
| 2 |
解答:
解:(1)作AB的中点F,连结EF,DF,
∵AB=2CD,
∴BE=CD=BC,
∵BE∥CD,
∴四边形BCDE为正方形,
∴DF⊥AB,
∵BE=AE,F为AB的中点,
∴EF⊥AB,
∴AB⊥平面DEF,
∵DE?平面DEF,
∴AB⊥DE.
(2)∵BC=1,
∴AB=2BC=2,BE=
=
,BD=
BC=
,FE=BF=1,DF=BC=1
∴DE=
EF=
,
∴△BDE为等边三角形,边长为
,
∴S△BDE=
×
×
=
.
∵EF⊥AB,平面EAB⊥平面ABCD,
∴EF⊥面ABCD,即EF为点E到平面ABCD的距离,
∴SE-BCD=
•EF•S△BCD=
×1×
=
,
设点C到平面EBD的距离为d,
则SE-BCD=
•d•S△BDE=
•d•
=
,
∴d=
,即点C到平面EBD的距离为
.
∵AB=2CD,
∴BE=CD=BC,
∵BE∥CD,
∴四边形BCDE为正方形,
∴DF⊥AB,
∵BE=AE,F为AB的中点,
∴EF⊥AB,
∴AB⊥平面DEF,
∵DE?平面DEF,
∴AB⊥DE.
(2)∵BC=1,
∴AB=2BC=2,BE=
| 2 | ||
|
| 2 |
| 2 |
| 2 |
∴DE=
| 2 |
| 2 |
∴△BDE为等边三角形,边长为
| 2 |
∴S△BDE=
| 1 |
| 2 |
| ||
| 2 |
| 2 |
| ||
| 2 |
∵EF⊥AB,平面EAB⊥平面ABCD,
∴EF⊥面ABCD,即EF为点E到平面ABCD的距离,
∴SE-BCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
设点C到平面EBD的距离为d,
则SE-BCD=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 2 |
| 1 |
| 6 |
∴d=
| ||
| 3 |
| ||
| 3 |
点评:本题主要考查了线面垂直的判定定理及性质,棱锥的体积,点到面的距离的计算.在第二问中利用了等体积法求得点到面的距离.

练习册系列答案
相关题目
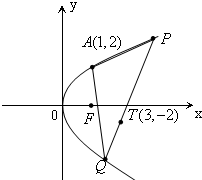 点A(1,2)到抛物线y2=2px(p>0)的焦点F的距离为2,过T(3,-2)的动直线l与此抛物线交于P、Q两点
点A(1,2)到抛物线y2=2px(p>0)的焦点F的距离为2,过T(3,-2)的动直线l与此抛物线交于P、Q两点 已知△ABC是边长为3的等边三角形,点D、E分别是边AB,AC上的点,且满足
已知△ABC是边长为3的等边三角形,点D、E分别是边AB,AC上的点,且满足 如图,四边形ABCD、BCFE、CDGF都是边长为1的正方形,M为棱AE上任意一点.
如图,四边形ABCD、BCFE、CDGF都是边长为1的正方形,M为棱AE上任意一点.