题目内容
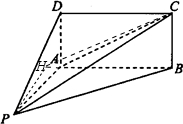
 如图,四棱锥P-ABCD的底面ABCD为矩形,且PA=AD=1,AB=2,∠PAB=120°,∠PBC=90°.
如图,四棱锥P-ABCD的底面ABCD为矩形,且PA=AD=1,AB=2,∠PAB=120°,∠PBC=90°.(Ⅰ)求证:平面PAD⊥平面PAB;
(Ⅱ)求四棱锥P-ABCD的体积;
(Ⅲ)求直线PC与平面ABCD所成角的正弦值.
考点:直线与平面所成的角,棱柱、棱锥、棱台的体积,平面与平面垂直的判定
专题:空间位置关系与距离
分析:(I)利用线线垂直证明线面垂直,再根据面面垂直的判定定理证明平面PAD⊥平面PAB;
(II)过P作PH⊥BA,交BA的延长线于H,可证PH⊥平面ABCD,求得PH,利用棱锥的体积公式计算;
(III)由(II)可证∠PAH为PC与平面ABCD所成的角,求得PC的长,在Rt△PHC中,求sin∠PCH的值.
(II)过P作PH⊥BA,交BA的延长线于H,可证PH⊥平面ABCD,求得PH,利用棱锥的体积公式计算;
(III)由(II)可证∠PAH为PC与平面ABCD所成的角,求得PC的长,在Rt△PHC中,求sin∠PCH的值.
解答:
解:(I)证明:∵∠PBC=90°,∴BC⊥PB,
∵四边形ABCD为矩形,∴BC⊥AB,又AB∩PB=B,
∴BC⊥平面PAB,∵AD∥BC,
∴AD⊥平面PAB,AD?平面PAD,
∴平面PAD⊥平面PAB;
(II)过P作PH⊥BA,交BA的延长线于H,
∵AD⊥平面PAB,∴PH⊥AD,AD∩BA=A,
∴PH⊥平面ABCD,∵,∠PAB=120°,PA=1,
∴AH=
,PH=
,∴VP-ABCD=
×2×1×
=
;
(III)连接CH,∵PH⊥平面ABCD,∴CH为PC在平面ABCD中的射影,
∴∠PAH为PC与平面ABCD所成的角,
PB=
=
=
,
PC=
=2
,
在Rt△PHC中,sin∠PCH=
=
=
.
∴直线PC与平面ABCD所成角的正弦值为
.
∵四边形ABCD为矩形,∴BC⊥AB,又AB∩PB=B,
∴BC⊥平面PAB,∵AD∥BC,
∴AD⊥平面PAB,AD?平面PAD,
∴平面PAD⊥平面PAB;
(II)过P作PH⊥BA,交BA的延长线于H,
∵AD⊥平面PAB,∴PH⊥AD,AD∩BA=A,
∴PH⊥平面ABCD,∵,∠PAB=120°,PA=1,
∴AH=
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 3 |
| ||
| 2 |
| ||
| 3 |
(III)连接CH,∵PH⊥平面ABCD,∴CH为PC在平面ABCD中的射影,
∴∠PAH为PC与平面ABCD所成的角,
PB=
| PH2+BH2 |
|
| 7 |
PC=
| 7+1 |
| 2 |
在Rt△PHC中,sin∠PCH=
| PH |
| PC |
| ||||
2
|
| ||
| 8 |
∴直线PC与平面ABCD所成角的正弦值为
| ||
| 8 |

点评:本题考查了面面垂直的证明,考查了棱锥的体积计算及直线与平面所成角的求法,考查了学生的空间想象能力及推论论证能力,综合性强.

练习册系列答案
相关题目
在△ABC中,角A,B,C所对的边分别为5,7,8,则∠B的大小是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
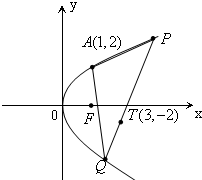 点A(1,2)到抛物线y2=2px(p>0)的焦点F的距离为2,过T(3,-2)的动直线l与此抛物线交于P、Q两点
点A(1,2)到抛物线y2=2px(p>0)的焦点F的距离为2,过T(3,-2)的动直线l与此抛物线交于P、Q两点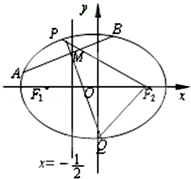 如图,F1,F2是离心率为
如图,F1,F2是离心率为 如图,四边形ABCD、BCFE、CDGF都是边长为1的正方形,M为棱AE上任意一点.
如图,四边形ABCD、BCFE、CDGF都是边长为1的正方形,M为棱AE上任意一点.