题目内容
在数列{an},{bn}中,a1=2,b1=4,且an,bn,an+1成等差数列,bn,an+1,bn+1成等比数列(n∈N*).
(1) 求a2,a3,a4及b2,b3,b4,由此猜测{an},{bn}的通项公式,并证明你的结论;
(2) 求证: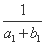 +
+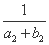 +…+
+…+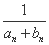 <
<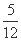 .
.
(1) 由题意得2bn=an+an+1,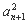 =bnbn+1,由此可得
=bnbn+1,由此可得
a2=6,b2=9,a3=12,b3=16,a4=20,b4=25.
猜测an=n(n+1),bn=(n+1)2.
用数学归纳法证明:
①当n=1时,由已知可得结论成立.
②假设当n=k时结论成立,即
ak=k(k+1),bk=(k+1)2.
那么当n=k+1时,
ak+1=2bk-ak=2(k+1)2-k(k+1)=(k+1)(k+2),
bk+1=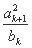 =(k+2)2.
=(k+2)2.
所以当n=k+1时,结论也成立.
由①②可知an=n(n+1),bn=(n+1)2对一切正整数都成立.
(2) 当n=1时,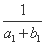 =
=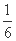 <
<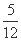 .
.
当n≥2时,由(1)知an+bn=(n+1)(2n+1)>2(n+1)n.
故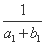 +
+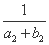 +…+
+…+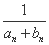
<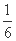 +
+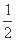 ×
×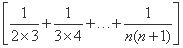
=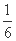 +
+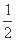 ×
×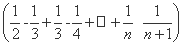
=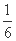 +
+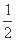 ×
×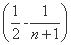 <
<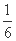 +
+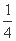 =
=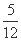 ,
,
综上,原不等式成立.

练习册系列答案
相关题目
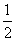 n(n+1) C.n2-1 D.
n(n+1) C.n2-1 D. ,则下列结论正确的是( )
,则下列结论正确的是( ) 是偶函数 (B)
是偶函数 (B) 上是增函数
上是增函数 
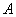 (0,-2),椭圆
(0,-2),椭圆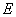 :
: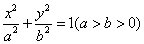 的离心率为
的离心率为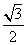 ,
,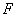 是椭圆的焦点,直线
是椭圆的焦点,直线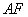 的斜率为
的斜率为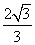 ,
,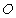 为坐标原点.
为坐标原点.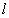 与
与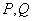 两点,当
两点,当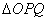 的面积最大时,求
的面积最大时,求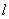 的方程.
的方程. =1(m<6)
=1(m<6) 与曲线
与曲线 =1(5<n<9)的( )
=1(5<n<9)的( ) -
- =1的焦点,PQ是过焦点F1的弦,那么|PF2|+|QF2|-
=1的焦点,PQ是过焦点F1的弦,那么|PF2|+|QF2|- |PQ|的值是__________.
|PQ|的值是__________. B.(x-1)2+(y-2)2=100
B.(x-1)2+(y-2)2=100