题目内容
已知点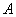 (0,-2),椭圆
(0,-2),椭圆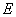 :
: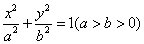 的离心率为
的离心率为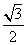 ,
,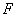 是椭圆的焦点,直线
是椭圆的焦点,直线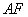 的斜率为
的斜率为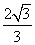 ,
, 为坐标原点.
为坐标原点.
(1) 求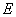 的方程;
的方程;
(2) 设过点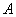 的直线
的直线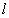 与
与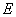 相交于
相交于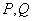 两点,当
两点,当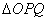 的面积最大时,求
的面积最大时,求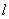 的方程.
的方程.
解:(Ⅰ) 显然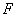 是椭圆的右焦点,设
是椭圆的右焦点,设
由题意

又离心率
 ,
,
故椭圆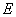 的方程为
的方程为 …………. …………4分
…………. …………4分
(Ⅱ) 由题意知,直线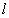 的斜率存在,设直线
的斜率存在,设直线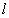 的斜率为
的斜率为 ,方程为
,方程为
联立直线与椭圆方程:  ,化简得:
,化简得:

设 ,则
,则 

坐标原点 到直线
到直线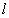 的距离为
的距离为

令  ,则
,则 
 (当且仅当
(当且仅当  即
即 时等号成立)
时等号成立)
故当  即
即  ,
, 时
时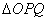 的面积最大
的面积最大
从而直线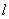 的方程为
的方程为  .…………. …………13分
.…………. …………13分

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
 B.
B. C.
C. D.
D.
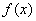 是定义在(-∞,+∞)上的偶函数,且在(-∞,0]上是增函数,设
是定义在(-∞,+∞)上的偶函数,且在(-∞,0]上是增函数,设 ,
, ,
, ,则
,则 的大小关系是( )
的大小关系是( ) B.
B.  C.
C.  D.
D. 
 ,且下列四个关系:
,且下列四个关系: ; ②
; ②  ; ③
; ③  ; ④
; ④  .
. 的个数是 .
的个数是 .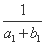 +
+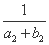 +…+
+…+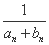 <
<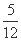 .
. +n=0间的距离是( )
+n=0间的距离是( )

 D.
D. 