题目内容
已知点P(2，－1)．
(1)求过点P且与原点距离为2的直线l的方程；
(2)求过点P且与原点距离最大的直线l的方程，最大距离是多少？
解析：(1)①当l的斜率k不存在时显然成立，此时l的方程为x＝2.
②当l的斜率k存在时，
设l：y＋1＝k(x－2)，即kx－y－2k－1＝0，
由点到直线的距离公式得
＝2，解得k＝
，
所以l：3x－4y－10＝0.
故所求l的方程为x＝2或3x－4y－10＝0.
(2)数形结合可得，过点P且与原点O距离最大的直线是过点P且与PO垂直的直线．
由l⊥OP，得klkOP＝－1，所以kl＝－
＝2.
由直
线方程的点斜式得直线l的方程为y＋1＝2(x－2)，
即2x－y－5＝0，
即直线2x－y－5＝0是过点P且与原点O距离最大的直线，最大距离为
＝
.
练习册系列答案
相关题目
B.
C.
D.
+
+…+
<
.
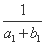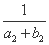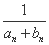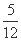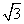x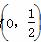 
的直线m交曲线E于A，B两点，过A，B两点分别作曲线E的切线，两切线交于点C，当△ABC的面积为2
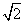时，求直线m的方程．
4x上任意一点，P在y轴上的射影为Q，点M(4,5)，则PQ与PM长度之和的最小值为( )
＋2 B.