题目内容
设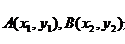 是椭圆
是椭圆 上的两点,已知向量
上的两点,已知向量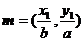 ,
,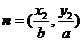 ,若
,若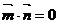 且椭圆的离心率
且椭圆的离心率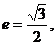 短轴长为2,
短轴长为2,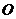 为坐标原点.
为坐标原点.
(1)求椭圆的方程;
(2)若直线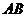 过椭圆的焦点
过椭圆的焦点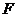 (0,c),(c为半焦距),求直线
(0,c),(c为半焦距),求直线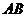 的斜率
的斜率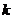 的值;
的值;
(3)试问: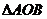 的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
解:(1)
椭圆的方程为
(2)由题意,设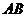 的方程为
的方程为

由已知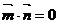 得:
得:



 ……7分
……7分
(3) ①当直线AB斜率不存在时,即 ,由
,由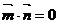

又  在椭圆上,所以
在椭圆上,所以

所以三角形的面积为定值.
②当直线AB斜率存在时:设AB的方程为y=kx+b






所以三角形的面积为定值.

练习册系列答案
相关题目
 (x2-3x+2)的单调递减区间是___________.
(x2-3x+2)的单调递减区间是___________.  为
为 所在平面上点,向量
所在平面上点,向量 ,
, 点
点 在线段
在线段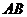 的垂直平分线上(垂足为
的垂直平分线上(垂足为 ),向量
),向量 若
若 ,则
,则 的值为 .
的值为 . 中,
中, 满足
满足 ,则点集
,则点集 所表示的区域的面积为( ).
所表示的区域的面积为( ). B.
B. C.
C. D.
D.
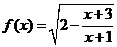 的定义域为
的定义域为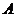 ,
,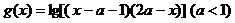 的定义域为
的定义域为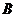 .(1)求
.(1)求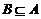 ,求实数
,求实数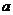 的取值范围.
的取值范围. 的是 ( )
的是 ( ) B.
B. ,
,
 D.
D.
 1相切,则圆C的方程是______
1相切,则圆C的方程是______ 与其关于点
与其关于点 对称的抛物线有两个不同的交点,若过这两个交点的直线的倾斜角为
对称的抛物线有两个不同的交点,若过这两个交点的直线的倾斜角为 ,则实数
,则实数 的值为______________.
的值为______________. 的前n项和为
的前n项和为 ,若
,若 ,则公差
,则公差 ___________.
___________.