题目内容
1.已知函数f(x)=e2x-t,g(x)=tex-1,对任意x∈R,f(x)≥g(x)恒成立,则实数t的取值范围为( )| A. | t≤1 | B. | t≤2$\sqrt{2}$-2 | C. | t≤2 | D. | t≤2$\sqrt{3}$-3 |
分析 设F(x)=f(x)-g(x),则F(x)=f(x)-g(x)=e2x-tex+1-t对任意x∈R,最小值为0,由此能求出实数t的取值范围.
解答 解:设F(x)=f(x)-g(x),
∵函数f(x)=e2x-t,g(x)=tex-1,对任意x∈R,f(x)≥g(x)恒成立,
∴F(x)=f(x)-g(x)=e2x-tex+1-t对任意x∈R,最小值为0,
F′(x)=2e2x-tex,由F′(x)=0,得x=ln$\frac{t}{2}$,
∴F(ln$\frac{t}{2}$)=${e}^{2ln\frac{t}{2}}$-te${\;}^{ln\frac{t}{2}}$+1-t≥0,
整理,得t2+4t-4≤0,
解得-2-2$\sqrt{2}$<t<2$\sqrt{2}$-2.
故选:B.
点评 本题考查实数的取值范围的求法,考查逻辑推理谁能力,运算求解能力,考查化归转化思想.是中档题,解题时要认真审题,注意导数性质的合理运用.

练习册系列答案
相关题目
12.已知直线l在平面α内,则“l⊥β”是“α⊥β”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
9. 某中学举行了一次“环保知识竞赛”,全校学生参加了这次竞赛,为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计,请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题:
某中学举行了一次“环保知识竞赛”,全校学生参加了这次竞赛,为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计,请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题:
(1)写出a,b,x,y的值.
(2)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取2名同学到广场参加环保知识的志愿宣传活动.
①求所抽取的2名同学中至少有1名同学的成绩在[90,100]内的概率;
②求所抽取的2名同学来自同一组的概率.
 某中学举行了一次“环保知识竞赛”,全校学生参加了这次竞赛,为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计,请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题:
某中学举行了一次“环保知识竞赛”,全校学生参加了这次竞赛,为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计,请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题:| 组别 | 分组 | 频数 | 频率 |
| 第1组 | [50,60) | 8 | 0.16 |
| 第2组 | [60,70) | a | ■ |
| 第3组 | [70,80) | 20 | 0.40 |
| 第4组 | [80,90) | ■ | 0.08 |
| 第5组 | [90,100] | 2 | b |
| 合计 | ■ | ■ |
(2)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取2名同学到广场参加环保知识的志愿宣传活动.
①求所抽取的2名同学中至少有1名同学的成绩在[90,100]内的概率;
②求所抽取的2名同学来自同一组的概率.
16.在△ABC中,角A,B,C所对的边分别为a,b,c,且bcosC+ccosB=$\sqrt{2}$acosC,则角C为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
6.已知a>b,c∈R,则( )
| A. | $\frac{1}{a}$<$\frac{1}{b}$ | B. | |a|>|b| | C. | a3>b3 | D. | ac>bc |
11.设点A,B的坐标分别为(4,0),(-4,0),直线AP,BP相交于点P,且它们的斜率之积为实数m,关于点P的轨迹下列说法正确的是( )
| A. | 当m<-1时,轨迹为焦点在x轴上的椭圆(除与x轴的两个交点) | |
| B. | 当-1<m<0时,轨迹为焦点在y轴上的椭圆(除与y轴的两个交点) | |
| C. | 当m>0时,轨迹为焦点在x轴上的双曲线(除与x轴的两个交点) | |
| D. | 当0<m<1时,轨迹为焦点在y轴上的双曲线(除与y轴的两个交点) |
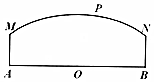 如图,两个工厂A,B相距8(单位:百米),O为AB的中点,曲线段MN上任意一点P到A,B的距离之和为10(单位:百米),且MA⊥AB,NB⊥AB.现计划在P处建一公寓,需考虑工厂A,B对它的噪音影响.工厂A对公寓的“噪音度”与距离AP成反比,比例系数为1;工厂B对公寓的“噪音度”与距离BP成反比,比例系数为k.“总噪音度”y是两个工厂对公寓的“噪音度”之和.经测算:当P在曲线段MN的中点时,“总噪音度”y恰好为1.
如图,两个工厂A,B相距8(单位:百米),O为AB的中点,曲线段MN上任意一点P到A,B的距离之和为10(单位:百米),且MA⊥AB,NB⊥AB.现计划在P处建一公寓,需考虑工厂A,B对它的噪音影响.工厂A对公寓的“噪音度”与距离AP成反比,比例系数为1;工厂B对公寓的“噪音度”与距离BP成反比,比例系数为k.“总噪音度”y是两个工厂对公寓的“噪音度”之和.经测算:当P在曲线段MN的中点时,“总噪音度”y恰好为1.