题目内容
4.设Sn,Tn分别是数列{an}和{bn}的前n项和,已知对于任意n∈N*,都有3an=2Sn+3,数列{bn}是等差数列,且T5=25,b10=19.(Ⅰ)求数列{an}和{bn}的通项公式;
(Ⅱ)设cn=$\frac{{{a}_{n}b}_{n}}{n(n+1)}$,求数列{cn}的前n项和Rn.
分析 (I)3an=2Sn+3,∴利用递推关系与等比数列的通项公式即可得出an.利用等差数列的通项公式与求和公式即可得出bn.
(II)cn=$\frac{{{a}_{n}b}_{n}}{n(n+1)}$=$\frac{{3}^{n}(2n-1)}{n(n+1)}$=$\frac{{3}^{n}[3n-(n+1)]}{n(n+1)}$=$\frac{{3}^{n+1}}{n+1}$-$\frac{{3}^{n}}{n}$,利用“裂项求和”方法即可得出.
解答 解:(I)∵3an=2Sn+3,∴n≥2时,3an-1=2Sn-1+3,
相减可得:3an-3an-1=2an,化为:an=3an-1,
n=1时,可得3a1=2a1+3,解得a1=3.
∴数列{an}是等比数列,首项与公比都为3.
∴an=3n.
设等差数列{bn}的公差为d,∵T5=25,b10=19.
∴5b1+$\frac{5×4}{2}$×d=25,b1+9d=19,
联立解得:b1=1,d=2.
∴bn=1+2(n-1)=2n-1.
(II)cn=$\frac{{{a}_{n}b}_{n}}{n(n+1)}$=$\frac{{3}^{n}(2n-1)}{n(n+1)}$=$\frac{{3}^{n}[3n-(n+1)]}{n(n+1)}$=$\frac{{3}^{n+1}}{n+1}$-$\frac{{3}^{n}}{n}$,
∴数列{cn}的前n项和Rn=$(\frac{{3}^{2}}{2}-\frac{3}{1})$+$(\frac{{3}^{3}}{3}-\frac{{3}^{2}}{2})$+…+$(\frac{{3}^{n+1}}{n+1}-\frac{{3}^{n}}{n})$=$\frac{{3}^{n+1}}{n+1}$-3.
点评 本题考查了等差数列与等比数列的通项公式与求和公式及其性质、裂项求和、数列的递推关系,考查了推理能力与计算能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | x2+(y-3)2=5 | B. | x2+(y+3)2=5 | C. | (x-3)2+y2=5 | D. | (x+3)2+y2=5 |
| A. | i | B. | -i | C. | -1 | D. | 1 |
| A. | (1,$\sqrt{3}$] | B. | (1,$\frac{3}{2}$] | C. | [$\frac{3}{2}$,+∞) | D. | (3,+∞) |
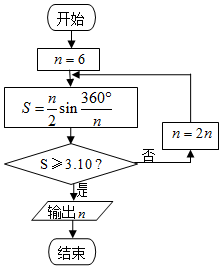 公元263年左右,我国古代数学家刘徽用圆内接正多边形的面积去逼近圆的面积求圆周率π,刘徽称这个方法为“割圆术”,并且把“割圆术”的特点概括为“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”下图是根据刘徽的“割圆术”思想设计的一个程序框图.若运行该程序,则输出的n的值为:(参考数据:$\sqrt{3}$≈1.732,sin15°≈0.2588,sin7.5°≈0.1305)( )
公元263年左右,我国古代数学家刘徽用圆内接正多边形的面积去逼近圆的面积求圆周率π,刘徽称这个方法为“割圆术”,并且把“割圆术”的特点概括为“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”下图是根据刘徽的“割圆术”思想设计的一个程序框图.若运行该程序,则输出的n的值为:(参考数据:$\sqrt{3}$≈1.732,sin15°≈0.2588,sin7.5°≈0.1305)( )